题目内容
【题目】已知函数
.
（1）求函数
的单调区间；
（2）如果对于任意的
， 
恒成立，求实数
的取值范围；
（3）设函数
， 
，过点
作函数
的图象的所有切线，令各切点的横坐标按从小到大构成数列
，求数列
的所有项之和的值.
【答案】（1）增区间为
；减区间为
.（2）
（3）
【解析】试题分析：（1）求单调区间则根据导数解不等式即可（2）令
要使
恒成立，只需当
时， 
分析函数单调性求出最小值解不等式即可（2）
设切点坐标为
，则切线斜率为
从而切线方程为
代入M
，令
， 
，这两个函数的图象均关于点
对称，则它们交点的横坐标也关于
对称，从而所作的所有切线的切点的横坐标构成数列
的项也关于
成对出现根据此规律即可分析得解
试题解析：
⑴
的增区间为
；减区间为
.
⑵令
要使
恒成立，只需当
时， 
令
，则
对
恒成立
在
上是增函数，则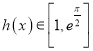
①当
时， 
恒成立， 
在
上为增函数
， 
满足题意；
②当
时， 
在
上有实根
, 
在
上是增函数
则当
时， 
， 
不符合题意；
③当
时， 
恒成立， 
在
上为减函数，
不符合题意
，即
.
⑶
设切点坐标为
，则切线斜率为
从而切线方程为
令
， 
，这两个函数的图象均关于点
对称，则它们交点的横坐标也关于
对称，从而所作的所有切线的切点的横坐标构成数列
的项也关于
成对出现，又在
共有1008对，每对和为
.
.
练习册系列答案
名校课堂系列答案
相关题目
