题目内容
已知四边形ABCD为矩形,PA⊥平面ABCD,M、N、E分别是AB、PC、CD的中点.(1)求证:MN∥平面PAD;
(2)当MN⊥平面PCD时,求二面角P-CD-B的大小.
(1)证明:取PD的中点为Q,连结AQ、QN,
∵N为PC的中点,
∴QN
DC.
∴QN
AM.
∴四边形AMNQ为平行四边形.
∴MN∥AQ.
∴MN∥平面PAD.
(2)解析:∵PA⊥平面ABCD,CD⊥AD,
∴PD⊥CD.
∴∠PDA为二面角PDCB的平面角.
∵MN⊥平面PCD,MN∥AQ,
∴AQ⊥平面PDC.∴AQ⊥PD.
∵Q为PD的中点,
∴△PAD为等腰直角三角形.
∴∠PDA=45°,即二面角P-CD-B的大小为45°.
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
如图，已知四边形ABCD为矩形，AD⊥平面ABE，AE=EB=BC=2，F为CE上的点，且BF⊥平面ACE．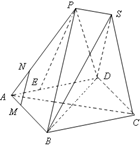
已知四边形ABCD为菱形，AB=6，∠BAD=60°，两个正三棱锥P-ABD、S-BCD（底面是正三角形且顶点在底面上的射影是底面正三角形的中心）的侧棱长都相等，如图，E、M、N分别在AD、
如图，已知四边形ABCD为直角梯形，∠ABC=90°，AD∥BC，AD=2，AB=BC=1，沿AC将△ABC折起，使点B到点P的位置，且平面PAC⊥平面ACD．
已知四边形ABCD为直角梯形，∠ADC=90°，AD∥BC，△ABD为等腰直角三角形，平面PAD⊥平面ABCD，E为PA的中点，AD=2BC=