Question

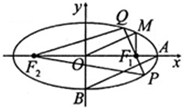（2012•安徽模拟）如图，椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)上的点M与椭圆右焦点F₁的连线MF₁与x轴垂直，且OM（O是坐标原点）与椭圆长轴和短轴端点的连线AB平行．
（1）求椭圆的离心率；
（2）过F₁且与AB垂直的直线交椭圆于P，Q，若△PF₂Q的面积是20

3

，求此时椭圆的标准方程．

Answer 1

分析：（1）由题设知M（c，

b2

a

），kOM=

b2

ac

，kAB=

b

a

，故

b2

ac

=

b

a

，由此能求出椭圆的离心率．
（2）设直线PQ的方程为：y=-

a

b

(x-c)，代入椭圆方程，消去x得：5y2-2

2

cy-2c2=0，故y1+y2  =

2 2 c

5

，y1y2=-

2c2

5

，所以(y1-y2)2=(

2 2 c

5

)2+

8c2

5

=

48c2

25

，由△PF₂Q的面积是20

3

，能求出椭圆的标准方程．

解答：解：（1）∵椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)上的点M与椭圆右焦点F₁的连线MF₁与x轴垂直，
且OM（O是坐标原点）与椭圆长轴和短轴端点的连线AB平行，
∴M（c，

b2

a

），kOM=

b2

ac

，kAB=

b

a

，
∴

b2

ac

=

b

a

，
∴b=c，∴a=

2

c，
∴e=

c

a

=

2

2

．
（2）设直线PQ的方程为：y=-

a

b

(x-c)，
即y=-

2

(x-c)，
代入椭圆方程，消去x得：

(c- y 2 )2

a2

+

y2

b2

=1，
整理，得：5y2-2

2

cy-2c2=0，
∴y1+y2  =

2 2 c

5

，y1y2=-

2c2

5

，
(y1-y2)2=(

2 2 c

5

)2+

8c2

5

=

48c2

25

，
∴S△PF2Q=

1

2

•2c•|y1-y2|=

4 3 c2

5

=20

3

，
∴c²=25，∴a²=50，b²=25，
所以椭圆方程为：

x2

50

+

y2

25

=1．

点评：本题考查椭圆的离心率和标准方程的求法，考查化归与转化、分类与整合的数学思想，培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识．