Question

已知圆C经过A（1，1）、B（2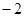，）两点，且圆心C在直线l：x-y+1=0上，求圆C的标准方程.

 

Answer 1

【答案】

（x+3）²+（y+2）²=25

【解析】

试题分析：设圆心坐标为C（a，a+1），根据A、B两点在圆上利用两点的距离公式建立关于a的方程，解出a值,从而算出圆C的圆心和半径，可得圆C的方程.

试题解析：∵圆心在直线x-y+1=0上，

∴设圆心坐标为C（a，a+1），

根据点A（1，1）和B（2，-2）在圆上，

可得(a−1)²+(a+1−1)²=(a−2)²+(a+1+2)²，

解之得a=-3,

∴圆心坐标为C（-3，2），

半径r²=(−3−1)²+(−3+1−1)²=25,

r=5,

∴此圆的标准方程是（x+3）²+（y+2）²=25．

考点：圆的标准方程.