题目内容
已知f(x)=xlnx, .
.
(1)当a=2时,求函数y=g(x)在[0,3]上的值域;
(2)求函数f(x)在[t,t+2](t>0)上的最小值;
(3)证明:对一切x∈(0,+∞),都有 成立.
成立.
解:(1)当a=2时,g(x)= ,x∈[0,3],
,x∈[0,3],
当x=1时, ;当x=3时,
;当x=3时, ,
,
故g(x)值域为 .
.
(2)f'(x)=lnx+1,当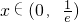 ,f'(x)<0,f(x)单调递减,
,f'(x)<0,f(x)单调递减,
当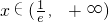 ,f'(x)>0,f(x)单调递增.
,f'(x)>0,f(x)单调递增.
①若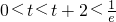 ,t无解;
,t无解;
②若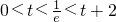 ,即
,即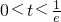 时,
时,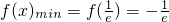 ;
;
③若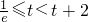 ,即
,即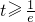 时,f(x)在[t,t+2]上单调递增,f(x)min=f(t)=tlnt,
时,f(x)在[t,t+2]上单调递增,f(x)min=f(t)=tlnt,
所以 f(x)min= .
.
(3)证明:令 h(x)= =
=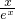 -
-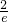 ,h′(x)=
,h′(x)=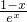 ,
,
当 0<x<1时,h′(x)>0,h(x)是增函数.当1<x时. h′(x)>0,h(x)是减函数,
故h(x) 在(0,+∞)上的最大值为h(1)=- .
.
而由(2)可得,f(x)=xlnx在(0,+∞)上的最小值为- ,
,
且当h(x) 在(0,+∞)上的最大值为h(1)时,f(x)的值为ln1=0,
故在(0,+∞)上恒有f(x)>h(x),即 .
.
分析:(1)当a=2时,由g(x)= ,x∈[0,3],利用二次函数的性质求出它的值域.
,x∈[0,3],利用二次函数的性质求出它的值域.
(2)利用函数f(x)的导数的符号,分类讨论f(x)单调性,从而求出f(x)的最小值.
(3)令 h(x)= =
=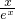 -
-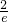 ,通过 h′(x)=
,通过 h′(x)=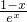 的符号研究h(x)的单调性,求出h(x)的最大值为h(1)=-
的符号研究h(x)的单调性,求出h(x)的最大值为h(1)=- .再由f(x)=xlnx在(0,+∞)上的最小值为-
.再由f(x)=xlnx在(0,+∞)上的最小值为- ,且f(1)=0大于h(1),可得在(0,+∞)上恒有f(x)>h(x),即
,且f(1)=0大于h(1),可得在(0,+∞)上恒有f(x)>h(x),即  .
.
点评:本题主要考查利用导数研究函数的单调性,二次函数的性质,函数的恒成立问题,属于中档题.
 ,x∈[0,3],
,x∈[0,3],当x=1时,
 ;当x=3时,
;当x=3时, ,
,故g(x)值域为
 .
.(2)f'(x)=lnx+1,当
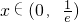 ,f'(x)<0,f(x)单调递减,
,f'(x)<0,f(x)单调递减,当
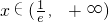 ,f'(x)>0,f(x)单调递增.
,f'(x)>0,f(x)单调递增. ①若
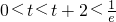 ,t无解;
,t无解; ②若
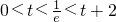 ,即
,即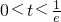 时,
时,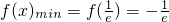 ;
; ③若
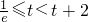 ,即
,即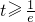 时,f(x)在[t,t+2]上单调递增,f(x)min=f(t)=tlnt,
时,f(x)在[t,t+2]上单调递增,f(x)min=f(t)=tlnt,所以 f(x)min=
 .
. (3)证明:令 h(x)=
 =
=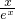 -
-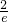 ,h′(x)=
,h′(x)=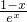 ,
,当 0<x<1时,h′(x)>0,h(x)是增函数.当1<x时. h′(x)>0,h(x)是减函数,
故h(x) 在(0,+∞)上的最大值为h(1)=-
 .
.而由(2)可得,f(x)=xlnx在(0,+∞)上的最小值为-
 ,
,且当h(x) 在(0,+∞)上的最大值为h(1)时,f(x)的值为ln1=0,
故在(0,+∞)上恒有f(x)>h(x),即
 .
.分析:(1)当a=2时,由g(x)=
 ,x∈[0,3],利用二次函数的性质求出它的值域.
,x∈[0,3],利用二次函数的性质求出它的值域.(2)利用函数f(x)的导数的符号,分类讨论f(x)单调性,从而求出f(x)的最小值.
(3)令 h(x)=
 =
=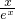 -
-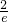 ,通过 h′(x)=
,通过 h′(x)=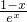 的符号研究h(x)的单调性,求出h(x)的最大值为h(1)=-
的符号研究h(x)的单调性,求出h(x)的最大值为h(1)=- .再由f(x)=xlnx在(0,+∞)上的最小值为-
.再由f(x)=xlnx在(0,+∞)上的最小值为- ,且f(1)=0大于h(1),可得在(0,+∞)上恒有f(x)>h(x),即
,且f(1)=0大于h(1),可得在(0,+∞)上恒有f(x)>h(x),即  .
.点评:本题主要考查利用导数研究函数的单调性,二次函数的性质,函数的恒成立问题,属于中档题.

练习册系列答案
相关题目