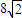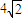Question

已知点P（x，y）到A（0，4）和B（-2，0）的距离相等，则2^x+4^y的最小值为

 

；此时x=

 

．

Answer 1

分析：先利用两点间的距离公式建立等式，化简求得点P的轨迹方程，然后利用基本不等式求得答案．

解答：解：题意得

(x-0)2+(y-4)2

=

(x+2)2+(y-0)2

，化简得点P的轨迹方程为x+2y=3.2^x+4^y=2^x+2^2y≥2

2x•22y

=2

2x+2y

=2

23

=4

2

．
最小值为4

2

．当2^x=2^2y时即x=

3

2

时等号成立，
故答案为：4

2

，

3

2

．

点评：本题主要考查了基本不等式在最值问题中的应用，两点间的距离公式．考查了学生对基础知识的综合运用，基本的运算能力．