Question

已知点P（x，y）到A（0，4）和B（-2，0）的距离相等，则2^x+4^y的最小值为（ ）
A．2
B．4
C．
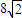
D．

Answer 1

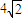
【答案】分析：首先根据因为点P（x，y）到A（0，4）和B（-2，0）的距离相等得到P在AB的垂直平分线上，然后求出垂线的方程，最后根据基本不等式求解．
解答：解：因为点P（x，y）到A（0，4）和B（-2，0）的距离相等
所以点P（x，y）在A，B的垂直平分线上，且过A  B的中点（-1，2）
所以垂线方程为：X+2Y-3=0 即X+2Y=3
因为2^X+4^Y=2^X+2^2Y，且2^x＞0，2^2y＞0，
所以2^x+4^y=2^x+2^2y≥==
所以最小值为，
故选D．
点评：本题考查两点间的距离公式，以及基本不等式的应用，通过对题目的分析抽象出数学模型，属于基础题．