题目内容
已知函数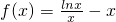 .
.
(1)求函数f(x)的单调区间;
(2)设m>0,求f(x)在[m,2m]上的最大值;
(3)试证明:对任意n∈N+,不等式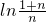 <
<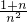 恒成立.
恒成立.
(1)解:求导函数可得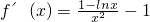 =-
=-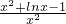
令g(x)=x2+lnx-1,x∈(0,+∞),则g′(x)=2x+ >0,∴函数g(x)在(0,+∞)上单调递增
>0,∴函数g(x)在(0,+∞)上单调递增
∵x=1时,f′(x)=0,∴x=1是f′(x)=0的唯一解
∵当0<x<1时,f′(x)>0;当x>1时,f′(x)<0
∴函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减
(2)解:由(1)知,函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减
①当0<2m≤1时,即0<m≤ 时,f(x)在[m,2m]上单调递增
时,f(x)在[m,2m]上单调递增
∴f(x)max=f(2m)=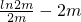
②当m≥1时,f(x)在[m,2m]上单调递减
∴f(x)max=f(m)=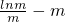
③当m<1<2m,即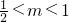 时,f(x)max=f(1)=-1
时,f(x)max=f(1)=-1
(3)证明:由(1)知,当x∈(0,+∞)时,f(x)max=f(1)=-1
∴在(0,+∞)上恒有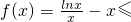 -1,当且仅当x=1时,等号成立
-1,当且仅当x=1时,等号成立
∴对任意的x∈(0,+∞)恒有lnx≤x(x-1)
∵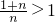 ,
,
∴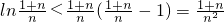
∴对任意n∈N+,不等式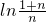 <
<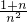 恒成立.
恒成立.
分析:(1)求导函数,确定x=1是f′(x)=0的唯一解,进而利用当0<x<1时,f′(x)>0;当x>1时,f′(x)<0,即可得到函数的单调区间;
(2)利用函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,对m进行分类讨论,确定函数的单调性,即可求得f(x)在[m,2m]上的最大值;
(3)证明在(0,+∞)上恒有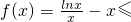 -1,当且仅当x=1时,等号成立,即可证得结论.
-1,当且仅当x=1时,等号成立,即可证得结论.
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,考查不等式的证明,解题的关键是确定函数的单调性,属于中档题.
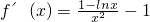 =-
=-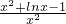
令g(x)=x2+lnx-1,x∈(0,+∞),则g′(x)=2x+
 >0,∴函数g(x)在(0,+∞)上单调递增
>0,∴函数g(x)在(0,+∞)上单调递增∵x=1时,f′(x)=0,∴x=1是f′(x)=0的唯一解
∵当0<x<1时,f′(x)>0;当x>1时,f′(x)<0
∴函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减
(2)解:由(1)知,函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减
①当0<2m≤1时,即0<m≤
 时,f(x)在[m,2m]上单调递增
时,f(x)在[m,2m]上单调递增∴f(x)max=f(2m)=
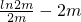
②当m≥1时,f(x)在[m,2m]上单调递减
∴f(x)max=f(m)=
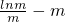
③当m<1<2m,即
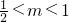 时,f(x)max=f(1)=-1
时,f(x)max=f(1)=-1(3)证明:由(1)知,当x∈(0,+∞)时,f(x)max=f(1)=-1
∴在(0,+∞)上恒有
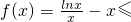 -1,当且仅当x=1时,等号成立
-1,当且仅当x=1时,等号成立∴对任意的x∈(0,+∞)恒有lnx≤x(x-1)
∵
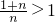 ,
,∴
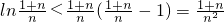
∴对任意n∈N+,不等式
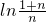 <
<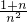 恒成立.
恒成立.分析:(1)求导函数,确定x=1是f′(x)=0的唯一解,进而利用当0<x<1时,f′(x)>0;当x>1时,f′(x)<0,即可得到函数的单调区间;
(2)利用函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,对m进行分类讨论,确定函数的单调性,即可求得f(x)在[m,2m]上的最大值;
(3)证明在(0,+∞)上恒有
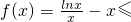 -1,当且仅当x=1时,等号成立,即可证得结论.
-1,当且仅当x=1时,等号成立,即可证得结论.点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,考查不等式的证明,解题的关键是确定函数的单调性,属于中档题.

练习册系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.