题目内容
函数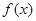 对任意的
对任意的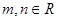 ,都有
,都有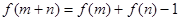 ,并且
,并且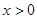 时,恒有
时,恒有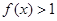 .
.
(Ⅰ)求证: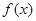 在
在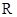 上是增函数;
上是增函数;
(Ⅱ)若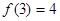 ,解不等式
,解不等式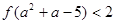 .
.
【答案】
(Ⅰ)见解析; (Ⅱ)a∈(-3,2).
【解析】(1)本题关于是利用m,n的取值的任意性,根据定义进行证明.
设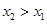 ,则
,则 .
.
(2)解本小题的关键是求出f(x)=2,对应的x的值.
由于f(3)=4,f(1+2)=f(1)+f(2)-1=f(1)+f(1)+f(1)-2=4,所以f(1)=2,所以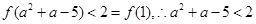 ,问题到此基本得以解决.
,问题到此基本得以解决.
(Ⅰ)证明 设x1<x2,∴x2-x1>0,
当x>0时,f(x)>1,∴f(x2-x1)>1. f(x2)=f[(x2-x1)+x1]=f(x2-x1)+f(x1)-1,
∴f(x2)-f(x1)=f(x2-x1)-1>0⇒f(x1)<f(x2),∴f(x)在R上为增函数.
(Ⅱ)解 ∵m,n∈R,不妨设m=n=1,∴f(1+1)=f(1)+f(1)-1⇒f(2)=2f(1)-1, f(3)=4⇒f(2+1)=4⇒f(2)+f(1)-1=4⇒3f(1)-2=4,∴f(1)=2,f(2)=2×2-1=3,
∴f(a2+a-5)<2=f(1),∵f(x)在R上为增函数,∴a2+a-5<1⇒-3<a<2,即
a∈(-3,2).

练习册系列答案
相关题目
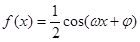 对任意的
对任意的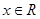 ,都有
,都有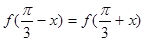 ,若函数
,若函数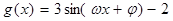 ,则
,则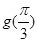 的值是( )
的值是( )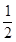
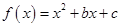 对任意的实数
对任意的实数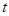 都有
都有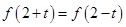 ,则( )
,则( )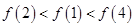 (B)
(B) 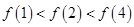
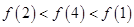 (D)
(D) 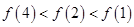
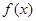 对任意的实数
对任意的实数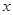 都有
都有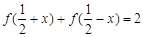 成立,则
成立,则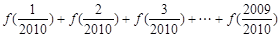 =
.
=
.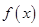 对任意的
对任意的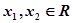 ,都有
,都有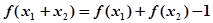 成立,且当
成立,且当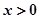 时,
时,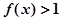 。
。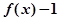 为奇函数;
为奇函数;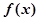 是R上的增函数;
是R上的增函数;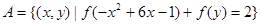 ,
,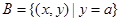 ,且
,且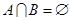 ,
求实数
,
求实数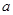 的取值范围。
的取值范围。