题目内容
已知数列{an}满足a1>0,an+1=2-|an|,n∈N*.
(Ⅰ)若a1,a2,a3成等比数列,求a1的值;
(Ⅱ)是否存在a1,使数列{an}为等差数列?若存在,求出所有这样的a1;若不存在,说明理由.
解:(Ⅰ)∵a1>0,∴a2=2-|a1|=2-a1,a3=2-|a2|=2-|2-a1|.
当0<a1≤2时,a3=2-(2-a1)=a1,∴a =(2-a1)2,解得a1=1.
=(2-a1)2,解得a1=1.
当a1>2时,a3=2-(a1-2)=4-a1,∴a1(4-a1)=(2-a1)2,解得a1=2-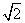 (舍去)或a1=2+
(舍去)或a1=2+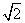 .
.
综上可得a1=1或a1=2+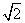 .
.
(Ⅱ)假设这样的等差数列存在,则
由2a2=a1+a3,得2(2-a1)=a1+(2-|2-a1|),即|2-a1|=3a1-2.
当a1>2时,a1-2=3a1-2,解得a1=0,与a1>2矛盾;
当0<a1≤2时,2-a1=3a1-2,解得a1=1,从而an=1(n∈N*),此时{an}是一个等差数列;
综上可知,当且仅当a1=1时,数列{an}为等差数列.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 是椭圆
是椭圆 的左、右焦点,
的左、右焦点,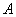 是椭圆短轴的一个端点,
是椭圆短轴的一个端点, 是椭圆上任意一点,过
是椭圆上任意一点,过 引
引 的外角平分线的垂线,垂足为
的外角平分线的垂线,垂足为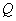 ,则
,则 的最大值为 .
的最大值为 . 
 与点
与点 重合,则与点
重合,则与点 重合的点是
重合的点是 B.
B. C.
C. D.
D.
 )n(n∈N*)的展开式的第3项的二项式系数为36,则其展开式中的常数项为
)n(n∈N*)的展开式的第3项的二项式系数为36,则其展开式中的常数项为
 ,
, ,则
,则 所含的元素个数为( )
所含的元素个数为( ) 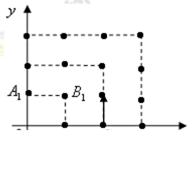 2010年,我国南方省市遭遇旱涝灾害,为防洪抗旱,某地区大面积植树造林,如图,在区域
2010年,我国南方省市遭遇旱涝灾害,为防洪抗旱,某地区大面积植树造林,如图,在区域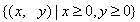 内植树,第一棵树在
内植树,第一棵树在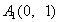 点,第二棵树在
点,第二棵树在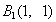 点,第三棵树在
点,第三棵树在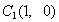 点,第四棵树在
点,第四棵树在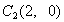 点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是( )
点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是( )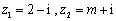
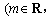
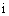 为虚数单位
为虚数单位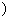 ,若
,若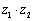 为实数,则
为实数,则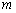 的值为 .
的值为 .