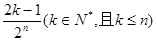题目内容
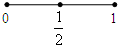 以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,1]对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标
以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,1]对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据题意,可知下一次的操作把上一次的对应点正好扩大了2倍.因为第一次操作后,原线段AB上的
,
均变成
,则第二次操作后,恰好被拉到与1重合的点所对应的数是
和
,则它们的和可求.根据题意,将恰好被拉到与1重合的点所对应的坐标列出数据,找出规律,列出通式即可.
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
解答:解:∵第一次操作后,原线段AB上的
,
,均变成
,
∴对应点扩大了2倍,
则第二次操作后,恰好被拉到与1重合的点所对应的数是
和
,
根据题意,得
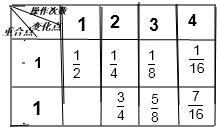
由上图表格,可以推出第n次操作后,恰好被拉到与1重合的点所对应的数的通式为为
,
.
所以恰好被拉到与1重合的点所对应的坐标为
,
,
,…
,
.
故选A.
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
∴对应点扩大了2倍,
则第二次操作后,恰好被拉到与1重合的点所对应的数是
| 1 |
| 4 |
| 3 |
| 4 |
根据题意,得

由上图表格,可以推出第n次操作后,恰好被拉到与1重合的点所对应的数的通式为为
| 1 |
| 2n |
| 2n-1 |
| 2n |
所以恰好被拉到与1重合的点所对应的坐标为
| 1 |
| 2 |
| 1 |
| 22 |
| 3 |
| 22 |
| 1 |
| 2n |
| 2n-1 |
| 2n |
故选A.
点评:此题的难点是理解题意,能够发现对应点之间的变化规律:下一次的操作把上一次的对应点正好扩大了2倍.解答本题的难点是根据数据列出通式,方便比较数据之间的联系,通过列表格的形式,可以直观一些.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,4]对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等).那么原闭区间[0,4]上(除两个端点外)的点,在第n次操作完成后(n≥1),恰好被拉到与4重合的点所对应的坐标为
以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,4]对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等).那么原闭区间[0,4]上(除两个端点外)的点,在第n次操作完成后(n≥1),恰好被拉到与4重合的点所对应的坐标为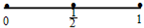 以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,1]对应的线段,对折后(坐标1所对应的点与原点重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标
以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,1]对应的线段,对折后(坐标1所对应的点与原点重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标 (2013•延庆县一模)以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,4]对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等).那么原闭区间[0,4]上(除两个端点外)的点,在第n次操作完成后(n≥1),恰好被拉到与4重合的点所对应的坐标为f(n),则f(3)=
(2013•延庆县一模)以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,4]对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等).那么原闭区间[0,4]上(除两个端点外)的点,在第n次操作完成后(n≥1),恰好被拉到与4重合的点所对应的坐标为f(n),则f(3)=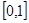 对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标
对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标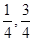 变成
变成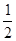 ,原来的坐标
,原来的坐标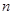 次操作完成后
次操作完成后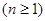 ,恰好被拉到与1重合的点对应的坐标是(
)
,恰好被拉到与1重合的点对应的坐标是(
)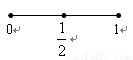
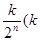 为
为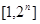 中所有奇数)
B.
中所有奇数)
B.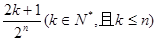
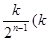 为
为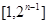 中所有奇数)
D.
中所有奇数)
D.