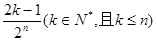题目内容
 以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,4]对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等).那么原闭区间[0,4]上(除两个端点外)的点,在第n次操作完成后(n≥1),恰好被拉到与4重合的点所对应的坐标为
以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,4]对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等).那么原闭区间[0,4]上(除两个端点外)的点,在第n次操作完成后(n≥1),恰好被拉到与4重合的点所对应的坐标为分析:在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4;这种操作实际上就是不断地把每条线段平分为两部分,每一部分的中点在操作之后对应的坐标都是2,末端与4重合,故可以归纳答案来.
解答:解:第一次操作后,原来的坐标1、3 变成2;原来的坐标2变成4;
第二次操作后,原来的坐标1、3 变成4,而2对应着第一次操作之前的0;
这种操作实际上就是不断地把每条线段平分为两部分,每一部分的中点在操作之后对应的坐标都是2,第一次操作之后,与4对应的点的坐标为2,只有1个;
第二次操作之后,与4对应的点应取0与2的中点1,2与4的中点3,共2个;
第三次操作之后,与4对应的点应取0与1的中点
,1与2的中点
,2与3的中点
,3与4的中点
,共4个,其坐标分别为
,
,
,
;
依此类推,第n次操作之后,与4对应的点的坐标应为:
,(其中j为[1,2n]中所有的奇数).
故答案为:
,(其中j为[1,2n]中所有的奇数).
第二次操作后,原来的坐标1、3 变成4,而2对应着第一次操作之前的0;
这种操作实际上就是不断地把每条线段平分为两部分,每一部分的中点在操作之后对应的坐标都是2,第一次操作之后,与4对应的点的坐标为2,只有1个;
第二次操作之后,与4对应的点应取0与2的中点1,2与4的中点3,共2个;
第三次操作之后,与4对应的点应取0与1的中点
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
依此类推,第n次操作之后,与4对应的点的坐标应为:
| j |
| 2n-2 |
故答案为:
| j |
| 2n-2 |
点评:本题主要考查了数列的实际应用以及归纳总结、分析推理的数学能力;解题时需要认真审题,仔细解答,以免出错.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,1]对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标
以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,1]对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,1]对应的线段,对折后(坐标1所对应的点与原点重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标
以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,1]对应的线段,对折后(坐标1所对应的点与原点重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标 (2013•延庆县一模)以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,4]对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等).那么原闭区间[0,4]上(除两个端点外)的点,在第n次操作完成后(n≥1),恰好被拉到与4重合的点所对应的坐标为f(n),则f(3)=
(2013•延庆县一模)以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间[0,4]对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等).那么原闭区间[0,4]上(除两个端点外)的点,在第n次操作完成后(n≥1),恰好被拉到与4重合的点所对应的坐标为f(n),则f(3)=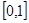 对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标
对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标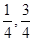 变成
变成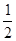 ,原来的坐标
,原来的坐标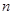 次操作完成后
次操作完成后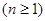 ,恰好被拉到与1重合的点对应的坐标是(
)
,恰好被拉到与1重合的点对应的坐标是(
)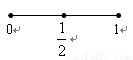
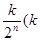 为
为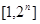 中所有奇数)
B.
中所有奇数)
B.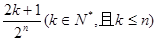
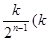 为
为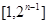 中所有奇数)
D.
中所有奇数)
D.