题目内容
已知n∈N*,实数a是常数,若
(
+
+…+
)=9,则a的值为( )
| lim |
| n→∞ |
| 4 |
| 1-a |
| 4a |
| 1-a |
| 4an |
| 1-a |
分析:直接利用数列求和,求出分子的和,然后应用极限的求法,得到a的方程,求出a的值.
解答:解:
+
+…+
=
(1+a+a2+…+an)
=
×
=
.
因为
(
+
+…+
)=9,
所以a∈(-1,1),
所以
=9,
解得a=
或
(舍去)
故选A.
| 4 |
| 1-a |
| 4a |
| 1-a |
| 4an |
| 1-a |
| 4 |
| 1-a |
=
| 4 |
| 1-a |
| 1-an+1 |
| 1-a |
=
| 4(1-an+1) |
| (1-a)2 |
因为
| lim |
| n→∞ |
| 4 |
| 1-a |
| 4a |
| 1-a |
| 4an |
| 1-a |
所以a∈(-1,1),
所以
| 4 |
| (1-a)2 |
解得a=
| 1 |
| 3 |
| 5 |
| 3 |
故选A.
点评:本题考查数列的极限的求法,数列前n项和的求法,考查计算能力.

练习册系列答案
相关题目
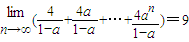 ,则a的值为( )
,则a的值为( )

 或
或
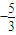 或
或
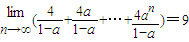 ,则a的值为( )
,则a的值为( )

 或
或
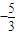 或
或