设直线y=ax+3与圆x2+y2-2x-4y+1=0相交于A.B两点.且.则a= ．题目和参考答案——青夏教育精英家教网—

题目内容

设直线y=ax+3与圆x²+y²-2x-4y+1=0相交于A，B两点，且

，则a= ．

【答案】分析：先确定圆心和半径，然后利用圆中的垂径定理求得圆心到直线的距离，从而简历关于a的方程，即可求得a的值．
解答：

解：圆的方程可化为：（x-1）²+（y-2）²=4∴圆心C（1，2）半径r=2
弦AB的中点为D，则|AD|=

，由圆的性质得圆心到直线的距离d=

=1
直线y=ax+3可化为ax-y+3=0∴C到直线的距离为

=1
解得：a=0
故答案为：0
点评：本题考查了直线与圆相交的性质，注意圆中的直角三角形的应用，避免联立直线与圆的方程，是个基础题．

练习册系列答案

新课标中考直通车系列答案

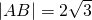设直线y=ax+3与圆x²+y²-2x-4y+1=0相交于A，B两点，且 $数学公式$ ，则a=________．