题目内容
已知函数f（x）=xn，其中n∈Z，n≥2．曲线y=f（x）在点P（x0，f（x0））（x0＞0）处的切线为l，l与x轴交于点Q，与y轴交于点R，则
=（ ）
| |PQ| |
| |PR| |
A．
| B．
| C．
| D．
|
由题可得f′（x）=nxn-1．
所以曲线y=f（x）在点（x0，f（x0））处的切线方程是：y-f（x0）=f′（x0）（x-x0）．
即y-x0n=nx0n-1（x-x0）．
令y=0，得-x0n=nx0n-1（x-x0）．
x0＞0，
∴x=x0-
，得l与x轴交点Q（x0-
，0），如图．
则
=
=
=
．
故选B．
所以曲线y=f（x）在点（x0，f（x0））处的切线方程是：y-f（x0）=f′（x0）（x-x0）．
即y-x0n=nx0n-1（x-x0）．
令y=0，得-x0n=nx0n-1（x-x0）．
x0＞0，
∴x=x0-
| x0 |
| n |
| x0 |
| n |
则
| |PQ| |
| |PR| |
| |PA| |
| |PB| |
|x0-
| ||
| |x0| |
| 1 |
| n |
故选B．
练习册系列答案
名校课堂系列答案
相关题目
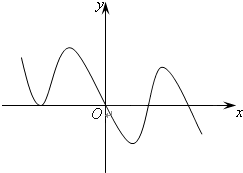
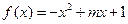在区间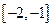
上的最大值就是函数的极大值，则
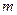的取值范围是 。