Question

若全称命题：“x∈［-1,+∞）时，x²-2ax+2≥a恒成立”，是真命题，求实数a的取值范围.

Answer 1

思路分析：由于此全称命题是真命题，所以可以推证出a的值，求出在x∈［-1,+∞）时，［f（x）］_min≥a或利用一元二次不等式与一元二次函数的关系解题.

解法一：由题意，x∈［-1,+∞），令f（x）=x²-2ax+2≥a都成立.?

∴f（x）=（x-a）²+2-a²可转化为x∈［-1,+∞），f（x）_min≥a成立，即x∈［-1,+∞）,?

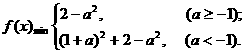
由f（x）的最小值f（x）_min≥a知，?

a∈［-3,1］.?

解法二：x²-2ax+2≥a，?

即x²-2ax+2-a≥0.?

令f（x）=x²-2ax+2-a，?

∴全称命题转化为x∈［-1,+∞）时，f（x）≥0成立.?

∴Δ≤0或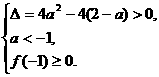

即-2≤a≤1或-3≤a＜-2?

∴-3≤a≤1.?

综上，所求实数a取值范围是［-3，1］.

温馨提示

由“恒成立”三个字即知是由全称量词构成的全称命题.由此来探讨“x∈［-1,+∞），?f（x）≥a?”只需f（x）_min≥a,解法二中等价转化为：x∈［-1,+∞），x²-2ax+2-a≥0成立，结合一元二次不等式的解集与图象间关系求解.