题目内容
17.已知实数a,b满足-2≤a≤2,-2≤b≤2,则函数y=$\frac{1}{3}$x3-$\frac{\sqrt{2}}{2}$ax2+bx-1有三个单调区间的概率为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 关键是要找出函数y=$\frac{1}{3}$x3-$\frac{\sqrt{2}}{2}$ax2+bx-1有三个单调区间,就是函数有2个极值点,求出对应的可行域面积的大小和实数a,b满足-2≤a≤2,-2≤b≤2对应的图形面积的大小.然后求解概率.
解答  解:∵函数y=$\frac{1}{3}$x3-$\frac{\sqrt{2}}{2}$ax2+bx-1有三个单调区间,就是函数有2个极值点,∴y′=x2-$\sqrt{2}$ax+b,存在2个零点,
解:∵函数y=$\frac{1}{3}$x3-$\frac{\sqrt{2}}{2}$ax2+bx-1有三个单调区间,就是函数有2个极值点,∴y′=x2-$\sqrt{2}$ax+b,存在2个零点,
即x2-$\sqrt{2}$ax+b=0有2个实数解,其充要条件是△=2a2-4b>0.
即 a2>2b.
如图所示,区域-2≤a≤2,-2≤b≤2的面积(图中正方形所示)为4
而区域a2≥b,
在条件-2≤a≤2,-2≤b≤2下的面积(图中阴影所示)为:
8+2∫02($\frac{1}{2}$)a2da=8+2×($\frac{1}{6}{a}^{3}$)|02=$\frac{32}{3}$.
所求概率为:$\frac{\frac{32}{3}}{16}$=$\frac{2}{3}$.
故选:D.
点评 本题考查函数的极值的求法,几何概型的概率估算公式中的“几何度量”,可以为线段长度、含面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据公式求解.

练习册系列答案
相关题目
10.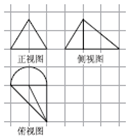 如图,在各小正方形边长为1的网格上依次为某几何体的正视图.侧视图与俯视图,其中正视图为等边三角形,则此几何体的体积为( )
如图,在各小正方形边长为1的网格上依次为某几何体的正视图.侧视图与俯视图,其中正视图为等边三角形,则此几何体的体积为( )
 如图,在各小正方形边长为1的网格上依次为某几何体的正视图.侧视图与俯视图,其中正视图为等边三角形,则此几何体的体积为( )
如图,在各小正方形边长为1的网格上依次为某几何体的正视图.侧视图与俯视图,其中正视图为等边三角形,则此几何体的体积为( )| A. | 1+$\frac{2π}{3}$ | B. | $\frac{4}{3}$+$\frac{2π}{3}$ | C. | $\frac{2\sqrt{3}}{3}$+$\frac{\sqrt{3}π}{6}$ | D. | $\frac{2\sqrt{3}}{3}$+$\frac{\sqrt{3}π}{3}$ |
2.设x∈R,向量$\overrightarrow{a}$=(x,1),$\overrightarrow{b}$=(4,-2),且$\overrightarrow{a}$$∥\overrightarrow{b}$,则|$\overrightarrow{a}+\overrightarrow{b}$|=( )
| A. | $\sqrt{5}$ | B. | 5 | C. | $\frac{\sqrt{85}}{2}$ | D. | $\frac{85}{4}$ |
9.将函数f(x)=sin2x的图象向左平移$\frac{π}{6}$个单位,再向上平移2个单位,得到g(x)的图象.若g(x1)•g(x2)=9,且x1,x2∈[-2π,2π],则|x1-x2|的最大值为( )
| A. | π | B. | 2π | C. | 3π | D. | 4π |
5.将函数$f(x)=sin(\frac{π}{2}-x)$的图象上所有点向左平行移动$\frac{π}{6}$个单位长度,得到函数g(x)的图象,则g(x)图象的一条对称轴的方程是( )
| A. | $x=\frac{π}{6}$ | B. | $x=\frac{π}{3}$ | C. | $x=\frac{2π}{3}$ | D. | $x=\frac{5π}{6}$ |
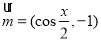 ,
,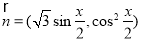 ,函数
,函数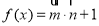 .
.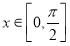 ,
,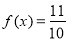 ,求
,求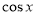 的值;
的值;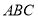 中,角
中,角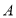 ,
,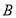 ,
,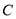 的对边分别是
的对边分别是 ,
,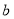 ,
,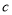 ,且满足
,且满足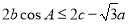 ,求角
,求角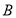 的取值范围.
的取值范围.