题目内容
由曲线y=f(x)(f(x)≤0),x∈[a,b],x=a,x=b(a<b)和x轴围成的曲边梯形的面积S=( )A.
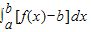
B.
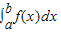
C.
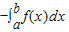
D.
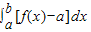
【答案】分析:根据积分的几何意义,得到曲边梯形的面积和积分的关系即可得到结论.
解答:解:因为f(x)≤0,所以由曲线y=f(x)(f(x)≤0),x∈[a,b],x=a,x=b(a<b)和x轴围成的曲边梯形的面积S等于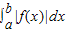 ,
,
因为f(x)≤0,所以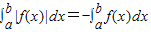 ,
,
故选C.
点评:本题主要考查定积分的应用,注意利用积分公式求面积时,必须要求被积函数为正.
解答:解:因为f(x)≤0,所以由曲线y=f(x)(f(x)≤0),x∈[a,b],x=a,x=b(a<b)和x轴围成的曲边梯形的面积S等于
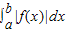 ,
,因为f(x)≤0,所以
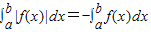 ,
,故选C.
点评:本题主要考查定积分的应用,注意利用积分公式求面积时,必须要求被积函数为正.

练习册系列答案
相关题目