题目内容
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若函数![]() 在区间
在区间![]() 内恰有一个零点,求
内恰有一个零点,求![]() 的取值范围;
的取值范围;
(3)设![]() ,当函数
,当函数![]() 的定义域为
的定义域为![]() 时,值域为
时,值域为![]() ,求a,b的值.
,求a,b的值.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】
(1)当![]() 时,不等式可化为
时,不等式可化为![]() ,解二次不等式,即可得答案;
,解二次不等式,即可得答案;
(2)由![]() ,
,![]() 知△
知△![]() ,从而可得
,从而可得![]() ,即
,即![]() ,再设
,再设![]() ,
,![]() ,从而由线性规划可得
,从而由线性规划可得![]() ,从而解得;
,从而解得;
(3)函数![]() 的对称轴
的对称轴![]() ,且开口向下,从而讨论以确定函数的最值,从而代入求解即可.
,且开口向下,从而讨论以确定函数的最值,从而代入求解即可.
![]() ,
,![]() ,
,
(1)当![]() 时,
时,
![]() ,
,
![]() ,即
,即![]() ,解得,
,解得,![]() ,
,
∴不等式的解集为:![]() .
.
(2)![]() ,
,![]() ,△
,△![]() ,
,
![]() 函数
函数![]() 的图象与
的图象与![]() 轴有2个交点,
轴有2个交点,
![]() 函数
函数![]() 在区间
在区间![]() 内恰有一个零点,
内恰有一个零点,
![]() ,即
,即![]() ,
,
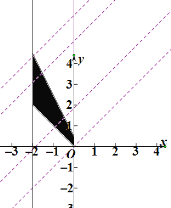
∴不等式组![]() 所表示的平面区域,如图所示的阴影部份,
所表示的平面区域,如图所示的阴影部份,
设![]() ,则
,则![]() ,
,
由图象可得:当直线![]() 过
过![]() 的直线的截距为0,过
的直线的截距为0,过![]() 的直线的截距为
的直线的截距为![]() ,
,
![]() ,即
,即![]() ,
,
故![]() 的范围为
的范围为![]() ,
,![]() ;
;
(3)![]() 函数
函数![]() ,
,![]() 对称轴
对称轴![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
即 ,解得
,解得![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
即 ,无解;
,无解;
综上所述,![]() ,
,![]() .
.

练习册系列答案
相关题目