题目内容

设an是（1+x）n的展开式中x2项的系数（n=2，3，4，…），则极限
lim
n→∞
(
1
a2
+…+
1
an
)=______．
二项展开式的通项Tr+1=Cnrxr
令r=2可得，an=Cn2=
n(n-1)
2

1
a2
+
1
a3
+…+
1
an
=2[
1
1×2
+
1
2×3
+…+
1
n(n-1)
]
=2(1-
1
2
+
1
2
-
1
3
+…
1
n-1
-
1
n
)
=2(1-
1
n
)
lim
n→∞
(
1
a2
+…+
1
an
)=
lim
n→∞
(2-
2
n
)=2
故答案为：2
练习册系列答案
相关题目
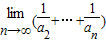设{an}是等差数列，其前n项的和为Sn．
（1）求证：数列{
Sn
n
}为等差数列；
（2）设{an}各项为正数，a1=
1
15
，a1≠a2，若存在互异正整数m，n，p满足：①m+p=2n；②
Sm
+
Sp
=2
Sn
．求集合{（x，y）|Sx•Sy=1，x∈N*，y∈N*}的元素个数；
（3）设bn=aan（a为常数，a＞0，a≠1，a1≠a2），数列{bn}前n项和为Tn．对于正整数c，d，e，f，若c＜d＜e＜f，且c+f=d+e，试比较（Tc）-1+（Tf）-1与（Td）-1+（Te）-1的大小．
设n∈N﹡且n≥2，若an是（1+x）n展开式中含x2项的系数，则
1
a2
+
1
a3
+…+
1
an
=
2(n-1)
n
2(n-1)
n
．
设an是（1+x）n的展开式中x2项的系数（n=2，3，4，…），则极限
lim
n→∞
(
1
a2
+…+
1
an
)=
2
2
．
设an是（1+x）n的展开式中x2项的系数（n=2，3，4，…），则极限=    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网