题目内容
双曲线
=1（a＞0，b＞0）的焦距为4，一个顶点是抛物线的y2=4x的焦点，则双曲线的离心率e等于
- A.2
- B.
- C.
- D.
A
分析：求出抛物线的y2=4x的焦点，确定双曲线的几何量，即可求得双曲线的离心率．
解答：由题意，抛物线的y2=4x的焦点是（1，0），所以a=1
∵双曲线=1（a＞0，b＞0）的焦距为4，
∴c=2
∴双曲线的离心率e=
=2
故选A．
点评：本题考查抛物线、双曲线的几何性质，考查学生的计算能力，属于基础题．
分析：求出抛物线的y2=4x的焦点，确定双曲线的几何量，即可求得双曲线的离心率．
解答：由题意，抛物线的y2=4x的焦点是（1，0），所以a=1
∵双曲线
=1（a＞0，b＞0）的焦距为4，∴c=2
∴双曲线的离心率e=
=2故选A．
点评：本题考查抛物线、双曲线的几何性质，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
=1（a＞0，b＞0）的离心率为
、F2分别为左、右焦点，M为左准线与渐近线在第二象限内的交点，且
．
（0＜m＜1）是x轴上的两点．过点A作斜率不为0的直线l，使得l交双曲线于C、D两点，作直线BC交双曲线于另一点E．证明直线DE垂直于x轴．中心O为圆心，分别以a和b为半径作大圆和．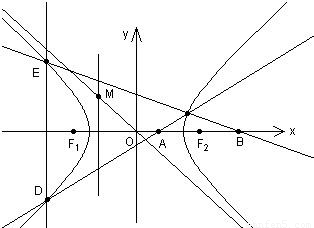
-
=1（a＞0，b＞0）的焦点，若在双曲线上存在点P，满足∠F1PF2=60°，|OP|=
a，则该双曲线的渐近线方程为（ ）
y=0
x±y=0
y=0
x±y=0
=1（a＞0，b＞0）的离心率为
，右准线方程为
．
-
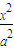=1（a＞0，b＞0）的焦点，若在双曲线上存在点P，满足∠F1PF2=60°，|OP|=
a，则该双曲线的渐近线方程为（ ）
y=0
x±y=0
y=0
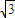x±y=0
=1（a＞0，b＞0）的离心率为
，右准线方程为
．