题目内容

设O为坐标原点，F1，F2是双曲线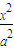-=1（a＞0，b＞0）的焦点，若在双曲线上存在点P，满足∠F1PF2=60°，|OP|=a，则该双曲线的渐近线方程为（ ）
A．x±y=0
B．x±y=0
C．x±y=0
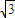D．x±y=0
【答案】分析：假设|F1P|=x，进而分别根据中线定理和余弦定理建立等式求得c2+5a2=14a2-2c2，求得a和c的关系，进而根据b=求得a和的关系进而求得渐进线的方程．
解答：解：假设|F1P|=x
OP为三角形F1F2P的中线，
根据三角形中线定理可知
x2+（2a+x）2=2（c2+7a2）
整理得x（x+2a）=c2+5a2
由余弦定理可知
x2+（2a+x）2-x（2a+x）=4c2
整理得x（x+2a）=14a2-2c2
进而可知c2+5a2=14a2-2c2
求得3a2=c2
∴c=a
b=a
那么渐近线为y=±x，即x±y=0
故选D
点评：本题将解析几何与三角知识相结合，主要考查了双曲线的定义、标准方程，几何图形、几何性质、渐近线方程，以及斜三角形的解法，属中档题
练习册系列答案
相关题目
设O为坐标原点，F1，F2是双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的焦点，若在双曲线上存在点P，满足∠F1PF2=60°，|OP|=
10
a，则该双曲线的渐近线方程为（　　）
A、x±
3
y=0
B、
3
x±y=0
C、x±
2
y=0
D、
2
x±y=0
设O为坐标原点，F1，F2是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点，若在椭圆上存在点P满足∠F1PF2=
π
3
，且|OP|=
3
2
a，则该椭圆的离心率为
1
2
1
2
．
设O为坐标原点，F1，F2是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的焦点，若在椭圆上存在点P，满足∠F1PF2=60°，|OP|=
3
2
a，则该椭圆的离心率为（　　）
设O为坐标原点，F1，F2是双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的焦点，若在双曲线上存在点P，满足∠F1PF2=60°，|OP|=
7
2
a，则该双曲线的离心率为（　　）
设O为坐标原点，F1，F2是双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的焦点，若在双曲线上存在点P，满足∠F1PF2=30°，|OP|=
7
a，则该双曲线的渐近线方程为？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网