题目内容
所有棱长都为2的正四面体的体积等于______．
当棱长为2时
正四面体的底面积S=
•22=
正四面体的高h=
•2=
故正四面体的体积V=
•S•h=
•
•
=
故答案为：
正四面体的底面积S=
| ||
| 4 |
| 3 |
正四面体的高h=
| ||
| 3 |
2
| ||
| 3 |
故正四面体的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
故答案为：
2
| ||
| 3 |
练习册系列答案
阅读快车系列答案
相关题目
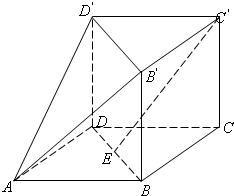如图，所有棱长都为2的正三棱柱BCD-B′C′D′，四边形ABCD是菱形，其中E为BD的中点．
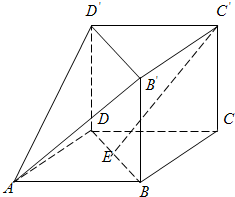如图，所有棱长都为2的正三棱柱BCD-B′C′D′，四边形ABCD是菱形，其中E为BD的中点．
，四边形
是菱形，其中
为
的中点。
(1) 求证：
；
面
；
与
的公共部分体积.
