Question

16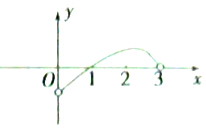．已知定义在区间（0，3）上的函数f（x）的图象如图所示，若$\overrightarrow{a}$=（f（x），0），$\overrightarrow{b}$=（cosx，1），则不等式$\overrightarrow{a}$•$\overrightarrow{b}$＜0的解集是（　　）

• A． （0，1）
• B． （0，1]
• C． （0，1）∪（$\frac{π}{2}$，3）
• D． （0，1]∪（$\frac{π}{2}$，3）

Answer 1

分析 分在（0，1）上、在（1，$\frac{π}{2}$）上、在（$\frac{π}{2}$，3）上三种情况，分别检验不等式是否成立，从而得出结论．

解答 解：不等式即 $\overrightarrow{a}$•$\overrightarrow{b}$=f（x）cosx＜0，结合f（x）的图象可得，
在（0，1）上，f（x）＜0，cosx＞0，满足不等式$\overrightarrow{a}$•$\overrightarrow{b}$＜0．
在（1，$\frac{π}{2}$）上，f（x）＞0，cosx＞0，不满足不等式$\overrightarrow{a}$•$\overrightarrow{b}$＜0．
在（$\frac{π}{2}$，3）上，f（x）＞0，cosx＜0，满足不等式$\overrightarrow{a}$•$\overrightarrow{b}$＜0．
综上可得，不等式$\overrightarrow{a}$•$\overrightarrow{b}$＜0 的解集为（0，1）∪（$\frac{π}{2}$，3），
故选：C．

点评 本题主要考查两个向量的数量积公式，余弦函数在各个象限中的符号，体现了分类讨论的数学思想，属于基础题．