题目内容
(本题满分16分;第(1)小题5分,第(2)小题5分,第(3)小题6分)
设 、
、 为坐标平面
为坐标平面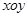 上的点,直线
上的点,直线 (
( 为坐标原点)与抛物线
为坐标原点)与抛物线 交于点
交于点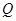 (异于
(异于 ).
).
(1)
若对任意 ,点
,点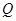 在抛物线
在抛物线 上,试问当
上,试问当 为何值时,点
为何值时,点 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程 ;
;
(2)
若点 在椭圆
在椭圆 上,试问:点
上,试问:点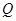 能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
(3)
对(1)中点 所在圆方程
所在圆方程 ,设
,设 、
、 是圆
是圆 上两点,且满足
上两点,且满足 ,试问:是否存在一个定圆
,试问:是否存在一个定圆 ,使直线
,使直线 恒与圆
恒与圆 相切.
相切.
(1)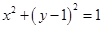 (2)
(2)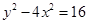 (3)
(3)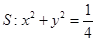
【解析】(1)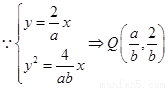 ,-----------------------------------------------------2分
,-----------------------------------------------------2分
代入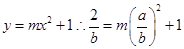
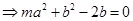 ----------------------------------
4分
----------------------------------
4分
当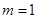 时,点
时,点 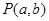 在圆
在圆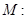
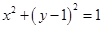 上-------------------------------------------5分
上-------------------------------------------5分
(2)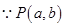 在椭圆
在椭圆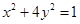 上,即
上,即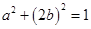
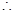 可设
可设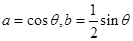 ------------------------------------------------------------------------7分
------------------------------------------------------------------------7分
又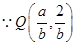 ,于是
,于是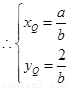
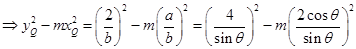
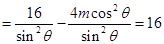 (令
(令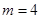 )
)
 点
点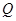 在双曲线
在双曲线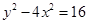 上--------------------------------------------------------------------10分
上--------------------------------------------------------------------10分
(3) 圆
圆 的方程为
的方程为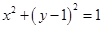
设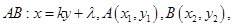 由
由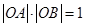
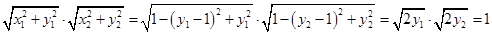
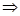
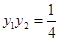 ----------------------------------------------------------------------------------------------12分[来源:Z,xx,k.Com]
----------------------------------------------------------------------------------------------12分[来源:Z,xx,k.Com]
又
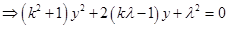 ,
,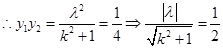 ------------14分
------------14分
又原点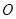 到直线
到直线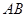 距离
距离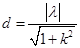
 ,即原点
,即原点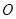 到直线
到直线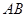 的距离恒为
的距离恒为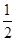
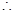 直线
直线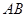 恒与圆
恒与圆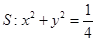 相切。---------------------------------------------------------16分
相切。---------------------------------------------------------16分

 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, ,
,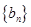 是等差数列,且
是等差数列,且 ,求非零常数
,求非零常数 ;
; ,求证:
,求证: .
.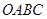 中,已知过点
中,已知过点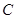 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若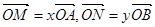 。
。 与
与 的关系为
的关系为 ;
; ,定义在
,定义在 上的偶函数
上的偶函数 ,当
,当 时
时 ,且函数
,且函数 对称,求证:
对称,求证: ,并求
,并求 时的解析式;
时的解析式; 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围。
的取值范围。 是
是 轴正方向的单位向量,设
轴正方向的单位向量,设 =
= ,
,  =
= ,且满足
,且满足 .
.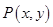 的轨迹方程;
的轨迹方程; 的直线
的直线 交上述轨迹于
交上述轨迹于 两点,且
两点,且 ,求直线
,求直线