题目内容
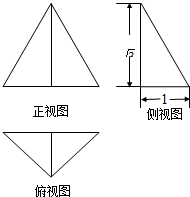
 5、已知三棱锥的三视图如图所示,则它的外接球表面积为( )
5、已知三棱锥的三视图如图所示,则它的外接球表面积为( )分析:由三棱锥的三视图我们可以得三棱锥的外接球半径为1,球心为俯视图斜边上的中点,则易求它的外接球表面积.
解答:解:由三棱锥的三视图我们易得俯视图斜边上的中点到三棱锥各顶点的距离均为1
所以三棱锥的外接球球心为俯视图斜边上的中点,半径为1
故它的外接球表面积为4π
故选C
所以三棱锥的外接球球心为俯视图斜边上的中点,半径为1
故它的外接球表面积为4π
故选C
点评:根据三视图判断空间几何体的形状,进而求几何的表(侧/底)面积或体积,是高考必考内容,处理的关键是准确判断空间几何体的形状,一般规律是这样的:如果三视图均为三角形,则该几何体必为三棱锥;如果三视图中有两个三角形和一个多边形,则该几何体为N棱锥(N值由另外一个视图的边数确定);如果三视图中有两个为矩形和一个多边形,则该几何体为N棱柱(N值由另外一个视图的边数确定);如果三视图中有两个为梯形和一个多边形,则该几何体为N棱柱(N值由另外一个视图的边数确定);如果三视图中有两个三角形和一个圆,则几何体为圆锥.如果三视图中有两个矩形和一个圆,则几何体为圆柱.如果三视图中有两个梯形和一个圆,则几何体为圆台.

练习册系列答案
相关题目
 已知三棱锥的三视图如图所示,其中侧视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于( )
已知三棱锥的三视图如图所示,其中侧视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|


 的三视图如图所示.
的三视图如图所示.
 是直角三角形;
是直角三角形; 求三棱锥
求三棱锥 在线段
在线段 上何处时,
上何处时, 与平面
与平面 所成的角为
所成的角为 .
.