题目内容
1.已知函数f ( x )=ln x和g(x)=$\frac{1}{2}{x^2}$+a(其中a为常数),直线l与f ( x ) 和g ( x )的图象都相切,且与f ( x ) 的图象的切点的横坐标为1.(Ⅰ)求l的方程和a的值;
(Ⅱ)记h ( x )=f ( x2+1)-g ( x )-ln 2,求函数h ( x ) 的极大值.
分析 (Ⅰ)求出函数f(x)的导函数,得到函数在x=1时的切线的斜率,由直线方程的点斜式求得切线方程,联立直线l与函数g(x),化为关于x的一元二次方程,利用判别式等于0求得a值;
(Ⅱ)把a值代入g(x)的解析式,进一步得到h ( x )=f ( x2+1)-g ( x )-ln 2,求其导函数,由导函数的符号得到函数的单调区间,从而求得函数的极大值.
解答 解:(Ⅰ)依题意,l与f (x)图象相切的切点为(1,0),
而f′(x)=$\frac{1}{x}$,∴kl=1,
从而l:y=x-1,
由$\left\{\begin{array}{l}{y=x-1}\\{y=\frac{1}{2}{x}^{2}+a}\end{array}\right.$,得x2-2x+2a+2=0,
判别式△=(-2)2-4×(2a+2)=0,解得a=-$\frac{1}{2}$;
(Ⅱ)记h(x)=f ( x2+1)-g(x)-ln2,
则h(x)=ln ( x2+1)-$\frac{1}{2}{x^2}+\frac{1}{2}$-ln2 (x∈R),
$h'(x)=\frac{2x}{{{x^2}+1}}-x=\frac{{x-{x^3}}}{{{x^2}+1}}$=$\frac{-(x+1)x(x-1)}{{{x^2}+1}}$,
令h'(x)<0,得(x+1)x(x-1)>0,即-1<x<0或x>1,
令h'(x)>0,得(x+1)x(x-1)<0,即x<-1或0<x<1.
∴h(x)在(-1,0),(1,+∞)上为减函数,在(-∞,-1),(0,1)上为增函数.
∴x=-1及x=1时,函数h(x)取得极大值,h(-1)=h(1)=0.
点评 本题考查利用导数研究函数的单调性,考查利用导数求函数的极值,是中档题.

| A. | a>b,c>d⇒a-c>b-d | B. | ac2>bc2⇒a>b | C. | ac<bc⇒a<b | D. | a>b⇒$\frac{a}{c}$>$\frac{b}{c}$ |
| A. | $\overrightarrow{AB}$=$\overrightarrow{DC}$ | B. | $\overrightarrow{AD}$+$\overrightarrow{AB}$=2$\overrightarrow{AO}$ | C. | $\overrightarrow{AD}$+$\overrightarrow{CB}$=$\overrightarrow 0$ | D. | $\overrightarrow{AB}$-$\overrightarrow{AD}$=$\overrightarrow{BD}$ |
| 损坏餐椅数 | 未损坏餐椅数 | 总 计 | |
| 学习雷锋精神前 | 50 | 150 | 200 |
| 学习雷锋精神后 | 30 | 170 | 200 |
| 总 计 | 80 | 320 | 400 |
(2)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
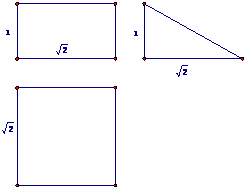 若某空间几何体的三视图如图所示.
若某空间几何体的三视图如图所示.