题目内容
【题目】【2015高考广东,文19】设数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() .已知
.已知![]() ,
,![]() ,
,![]() ,且当
,且当![]()
时,![]() .
.
(1)求![]() 的值;
的值;
(2)证明:![]() 为等比数列;
为等比数列;
(3)求数列![]() 的通项公式.
的通项公式.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)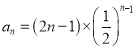 .
.
【解析】
试题分析:(1)令![]() 可得
可得![]() 的值;(2)先将
的值;(2)先将![]() (
(![]() )转化为
)转化为![]() ,再利用等比数列的定义可证
,再利用等比数列的定义可证![]() 是等比数列;(3)先由(2)可得数列
是等比数列;(3)先由(2)可得数列![]() 的通项公式,再将数列
的通项公式,再将数列![]() 的通项公式转化为数列
的通项公式转化为数列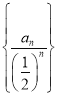 是等差数列,进而可得数列
是等差数列,进而可得数列![]() 的通项公式.
的通项公式.
试题解析:(1)当![]() 时,
时,![]() ,即
,即![]() ,解得:
,解得:![]()
(2)因为![]() (
(![]() ),所以
),所以![]() (
(![]() ),即
),即![]() (
(![]() ),因为
),因为![]() ,所以
,所以![]() ,因为
,因为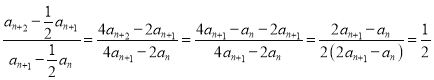 ,所以数列
,所以数列![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列
的等比数列
(3)由(2)知:数列![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列,所以
的等比数列,所以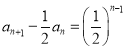
即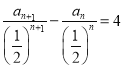 ,所以数列
,所以数列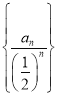 是以
是以![]() 为首项,公差为
为首项,公差为![]() 的等差数列,所以
的等差数列,所以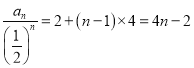 ,即
,即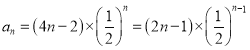 ,所以数列
,所以数列![]() 的通项公式是
的通项公式是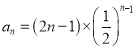

练习册系列答案
相关题目