题目内容
已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,CG垂直于ABCD所在的平面,且CG=2,求点B到平面EFG的距离.
解法一:(向量法)?
如图建立空间直角坐标系C—xyz.?
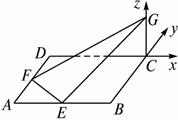
则G(0,0,2),E(-2,-4,0),F(-4,-2,0),B(0,-4,0),![]() =(-2,-4,-2),
=(-2,-4,-2),![]() =(-4,-2,-2),
=(-4,-2,-2),![]() =(-2,0,0).?
=(-2,0,0).?
设平面EFG的法向量为n=(x,y,z),?
由![]() ·n=0,
·n=0,![]() ·n=0,得?
·n=0,得?
x=-t,y=-t,z=3t,令t=1.?
即n=(-1,-1,3),于是点B到平面EFG的距离d=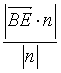 =
=![]() =
=![]() .
.
解法二:(等积变换)根据![]() 求之.设B点到平面EFG的距离为x.?
求之.设B点到平面EFG的距离为x.?
由平几知识易求EF=2![]() ,?
,?
GH=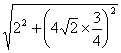 =
=![]() .?
.?
![]() =
=![]() ×2×2=2,
×2×2=2,![]() =
=![]() ×2
×2![]() ×
×![]() =2
=2![]() ,?
,?
由![]() ,得?
,得?
![]() ·
·![]() ·x=
·x=![]() ·
·![]() ?·GC,?
?·GC,?
即![]() ×2
×2![]() x=
x=![]() ×2×2,?
×2×2,?
解得x=![]() =
=![]() .?
.?
即点B到平面EFG的距离为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.
如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2. 如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.
如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.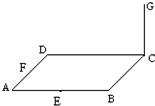 已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离.
已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离. 如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.
如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.