题目内容
已知直线y=-2x-| 2 |
| 3 |
| 1 |
| 3 |
(Ⅰ)求b的值;
(Ⅱ)若方程f(x)=x2+m在(0,+∞)上有两个解x1,x2,求m的取值范围.
分析:(I)先求出导函数f'(x),设出切点(x0,y0),然后根据在x=x0的导数等于切线的斜率,切点在切线和函数f(x)的图象上,建立方程组,解之即可求出b的值;
(II)构造函数h(x)=f(x)-x2-m=
x3-x2-3x-m,利用导数研究函数h(x)的单调性,转化成使h(x)图象在(0,+∞)内与x轴有两个不同的交点,建立关系式,解之即可求出m的范围.
(II)构造函数h(x)=f(x)-x2-m=
| 1 |
| 3 |
解答:解:(I)∵f(x)=
x3-bx,∴f'(x)=x2-b,
设切点为(x0,y0),依题意得∴
解得:b=3
(II)设h(x)=f(x)-x2-m=
x3-x2-3x-m
h′(x)=x2-2x-3=(x+1)(x-3),
令h′(x)=0,得x=-1或x=3
在(0,3)上,h′(x)<0,故h(x)在(0,3)上单调递减,
在(3,+∞)上,h′(x)>0,故h(x)在(3,+∞)上是单调递增,
若使h(x)图象在(0,+∞)内与x轴有两个不同的交点,
则需
∴-9<m<0.
此时存在x>3时,h(x)>0,
例如x=5时,h=
-25=15-m=
-m>0.
∴所求m的范围是-9<m<0.
| 1 |
| 3 |
设切点为(x0,y0),依题意得∴
|
解得:b=3
(II)设h(x)=f(x)-x2-m=
| 1 |
| 3 |
h′(x)=x2-2x-3=(x+1)(x-3),
令h′(x)=0,得x=-1或x=3
在(0,3)上,h′(x)<0,故h(x)在(0,3)上单调递减,
在(3,+∞)上,h′(x)>0,故h(x)在(3,+∞)上是单调递增,
若使h(x)图象在(0,+∞)内与x轴有两个不同的交点,
则需
|
此时存在x>3时,h(x)>0,
例如x=5时,h=
| 125 |
| 3 |
| 5 |
| 3 |
∴所求m的范围是-9<m<0.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及函数与方程的综合运用等基础题知识,考查运算求解能力、推理论证能力,考查化归与转化思想,属于基础题.

练习册系列答案
相关题目
已知直线y=2x上一点P的横坐标为a,有两个点A(-1,1),B(3,3),那么使向量
与
夹角为钝角的一个充分不必要条件是( )
| PA |
| PB |
| A、-1<a<2 | ||||||||
| B、0<a<1 | ||||||||
C、-
| ||||||||
| D、0<a<2 |
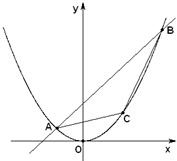 已知直线y=2x+k被抛物线x2=4y截得的弦长AB为20,O为坐标原点.
已知直线y=2x+k被抛物线x2=4y截得的弦长AB为20,O为坐标原点.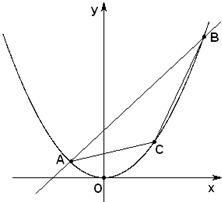 已知直线y=2x+1与抛物线x2=4y交于A,B两点,O为坐标原点.点C位于抛物线弧AOB上,求点C坐标使得△ABC面积最大.
已知直线y=2x+1与抛物线x2=4y交于A,B两点,O为坐标原点.点C位于抛物线弧AOB上,求点C坐标使得△ABC面积最大.