题目内容
【题目】已知椭圆![]() 的左右顶点分别是
的左右顶点分别是![]() ,
,![]() ,点
,点![]() 在椭圆上,过该椭圆上任意一点P作
在椭圆上,过该椭圆上任意一点P作![]() 轴,垂足为Q,点C在
轴,垂足为Q,点C在![]() 的延长线上,且
的延长线上,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)求动点C的轨迹E的方程;
(3)设直线![]() (C点不同A、B)与直线
(C点不同A、B)与直线![]() 交于R,D为线段
交于R,D为线段![]() 的中点,证明:直线
的中点,证明:直线![]() 与曲线E相切;
与曲线E相切;
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明略;
;(3)证明略;
【解析】
(1)根据顶点坐标可知![]() ,将
,将![]() 代入椭圆方程可求得
代入椭圆方程可求得![]() ,进而得到椭圆方程;(2)设
,进而得到椭圆方程;(2)设![]() ,
,![]() ,可得到
,可得到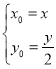 ,将
,将![]() 代入椭圆方程即可得到所求的轨迹方程;(3)设
代入椭圆方程即可得到所求的轨迹方程;(3)设![]() ,可得直线
,可得直线![]() 方程,进而求得
方程,进而求得![]() 和
和![]() 点坐标;利用向量坐标运算可求得
点坐标;利用向量坐标运算可求得![]() ,从而证得结论.
,从而证得结论.
(1)由题意可知:![]()
将![]() 代入椭圆方程可得:
代入椭圆方程可得:![]() ,解得:
,解得:![]()
![]() 椭圆
椭圆![]() 的方程为:
的方程为:![]()
(2)设![]() ,
,![]()
由![]() 轴,
轴,![]() 可得:
可得: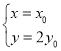 ,即
,即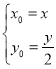
![]()
将![]() 代入椭圆
代入椭圆![]() 方程得:
方程得:![]()
![]() 动点
动点![]() 的轨迹
的轨迹![]() 的方程为:
的方程为:![]()
(3)设![]() ,则直线
,则直线![]() 方程为:
方程为:![]()
令![]() ,解得:
,解得:![]()
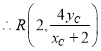

![]() ,
,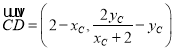
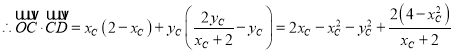
![]()
即![]()
![]() 直线
直线![]() 与曲线
与曲线![]() 相切
相切

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对100名出租车司机进行调查.调查问卷共10道题,答题情况如下表:
答对题目数 |
| 8 | 9 |
|
女 | 2 | 13 | 12 | 8 |
男 | 3 | 37 | 16 | 9 |
(1)如果出租车司机答对题目数大于等于9,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
(2)从答对题目数少于8的出租车司机中任选出两人做进一步的调查,求选出的两人中至少有一名女出租车司机的概率.
【题目】某种产品,每售出一吨可获利![]() 万元,每积压一吨则亏损
万元,每积压一吨则亏损![]() 万元.某经销商统计出过去
万元.某经销商统计出过去![]() 年里市场年需求量的频数分布表如下表所示.
年里市场年需求量的频数分布表如下表所示.
年需求量(吨) |
|
|
|
|
|
年数 |
|
|
|
|
|
(1)求过去![]() 年年需求量的平均值;(每个区间的年需求量用中间值代替)
年年需求量的平均值;(每个区间的年需求量用中间值代替)
(2)今年该经销商欲进货![]() 吨,以
吨,以![]() (单位:吨,
(单位:吨,![]() )表示今年的年需求量,以
)表示今年的年需求量,以![]() (单位:万元)表示今年销售的利润,试将
(单位:万元)表示今年销售的利润,试将![]() 表示
表示![]() 的函数解析式,并求今年的年利润不少于
的函数解析式,并求今年的年利润不少于![]() 万元的概率.
万元的概率.