Question

【题目】已知函数f（x）=（ax﹣1）lnx+ ． （Ⅰ）若a=2，求曲线y=f（x）在点（1，f（1））处的切线l的方程；
（Ⅱ）设函数g（x）=f'（x）有两个极值点x1 ， x2 ， 其中x1∈（0，e），求g（x1）﹣g（x2）的最小值．

Answer 1

【答案】解：（I）当a=2时， ，

得切线l的方程为 即4x﹣2y﹣3=0．

（II） ，定义域为（0，+∞），

，令g'（x）=0得x2+ax+1=0，

其两根为x1，x2，且x1+x2=﹣a，x1x2=1，

故 ．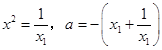

= ，

．

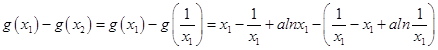
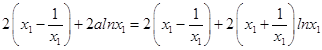则（g（x1）﹣g（x2））min=h（x）min， ，

当x∈（0，1]时，恒有h'（x）≤0，x∈（1，e]时，恒有h'（x）＜0，

总之当x∈（1，e]时，h（x）在x∈（0，e]上单调递减，

所以 ，

∴ ．

【解析】（Ⅰ）求出函数的导数，计算f（1），f′（1），求出切线方程即可；（Ⅱ）求出函数的导数，得到 ，求出g（x1）﹣g（x2）的解析式，根据函数的单调性求出其最小值即可．
【考点精析】利用函数的极值与导数对题目进行判断即可得到答案，需要熟知求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值．