题目内容
设点A,B的坐标分别为(-5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积为-2,则点M的轨迹是( )
分析:设出点M的坐标,表示出直线AM、BM的斜率,进而求出它们的斜率之积,利用斜率之积是-2,建立方程,去掉不满足条件的点,即可得到点M的轨迹方程.
解答:解:设M(x,y),因为A(-5,0),B(5,0)
所以kAM=
(x≠-5),kBM=
(x≠5)
由已知,
•
=-2
化简,得2x2+y2=50(x≠±5)
轨迹方程是椭圆.
故选B.
所以kAM=
| y |
| x+5 |
| y |
| x-5 |
由已知,
| y |
| x+5 |
| y |
| x-5 |
化简,得2x2+y2=50(x≠±5)
轨迹方程是椭圆.
故选B.
点评:本题重点考查轨迹方程的求解,解题的关键是正确表示出直线AM、BM的斜率,利用条件建立方程.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
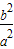 时,点M的轨迹是双曲线.(其中a,b∈R+)
时,点M的轨迹是双曲线.(其中a,b∈R+)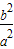 时,点M的轨迹是部分椭圆.(其中a,b∈R+)
时,点M的轨迹是部分椭圆.(其中a,b∈R+)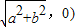 ,F2(
,F2(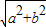 ,0),且|PF1|=
,0),且|PF1|= |PF2|,则(1)的轨迹所在的圆锥曲线的离心率取值范围(1,
|PF2|,则(1)的轨迹所在的圆锥曲线的离心率取值范围(1, ]
]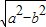 ,0),F2(
,0),F2(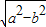 ,0).满足
,0).满足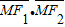 =0的点M总在曲线的内部,则(2)的轨迹所在的圆锥曲线的离心率的取值范围是
=0的点M总在曲线的内部,则(2)的轨迹所在的圆锥曲线的离心率的取值范围是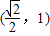 .
.