题目内容
已知△ABC的三边长分别是3、4、5,点P是它的内切圆上一点,求以PA、PB、PC分别为直径的三个圆面积之和的最大值和最小值.
解析:由已知得△ABC为直角三角形,建立如下图所示的直角坐标系,则A(0,0)、B(4,0)、C(0,3).
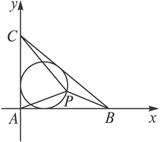
设内切圆半径为r,则r=
(a+b-c)=1,故内切圆的方程为(x-1)2+(y-1)2=1.
又设P点坐标为(1+cosα,1+sinα),以PA、PB、PC为直径的三个圆面积
S=π(
)2+π(
)2+π(
)2
=
(PA2+PB2+PC2)
=
［(1+cosα)2+(1+sinα)2+(1+cosα-4)2+(1+sinα)2+(1+cosα)2+(1+sinα-3)2］
=
(10-cosα),
又∵-1≤cosα≤1,∴当cosα=-1时,Smax=
;当cosα=1时,Smin=
.
练习册系列答案
相关题目
已知△ABC的三边长为a、b、c，满足直线ax+by+c=0与圆x2+y2=1相离，则△ABC是（ ）
| A、锐角三角形 | B、直角三角形 | C、钝角三角形 | D、以上情况都有可能 |