题目内容
已知F1、F2是椭圆C：
(a＞b＞0)的左、右焦点，c为半焦距，相邻两顶点的距离为
，椭圆
的离心率为
.
(Ⅰ)求椭圆的方程；
(Ⅱ)直线
与椭圆相交于
、
两点（、不是椭圆的顶点），以
为直径的圆过椭圆C与
轴的正半轴的交点，求
的值；
(Ⅲ)过F2的直线交椭圆C于M、N，求△MF1N面积的最大值.
解：（Ⅰ）由已知可得 
，
∴
∴椭圆的方程为 
. ……………………3分
（Ⅱ）设
、
两点的坐标分别为
、
.
将直线
代入椭圆方程中，整理得
∵⊿
∴
.
∴
∵以
为直径的圆过椭圆与
轴正半轴的交点
，
∴
∴
∴
∴
∴
整理得 
∴
，
当时，直线
过椭圆的一个顶点
，与已知矛盾，舍去.
∴
的值为
……………………8分
（Ⅲ）设
、
两点的坐标分别为
、
. 直线
与
轴夹角为
由
∴当
取得最大时，
取得最大值.
设过
的直线为
，
代入椭圆方程中，整理得
∴
.
∴
∴
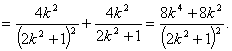
当不存在时，也满足上式.
∴
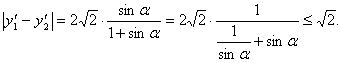
当且仅当
，即
时，等号成立.
∴
的面积的最大值为
. ……………………14分
练习册系列答案
寒假学与练系列答案
相关题目