题目内容
P(x0,y0)(x0≠±a)是双曲线E:
-
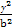=1(a>0,b>0)上一点,M,N分别是双曲线E的左,右顶点,直线PM,PN的斜率之积为
.
(1)求双曲线的离心率.
(2)过双曲线E的右焦点且斜率为1的直线交双曲线于A,B两点,O为坐标原点,C为双曲线上一点,满足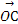
=λ
+
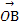,求λ的值.
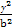-=1(a>0,b>0)上一点,M,N分别是双曲线E的左,右顶点,直线PM,PN的斜率之积为.(1)求双曲线的离心率.
(2)过双曲线E的右焦点且斜率为1的直线交双曲线于A,B两点,O为坐标原点,C为双曲线上一点,满足
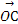=λ+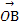,求λ的值.(1)
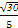(2) λ=0或λ=-4
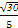(2) λ=0或λ=-4【思路点拨】(1)代入P点坐标,利用斜率之积为列方程求解.
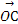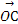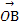(2)联立方程,设出A,B,的坐标,代入=λ+求解.
解：(1)由点P(x0,y0)(x0≠±a)在双曲线-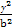=1上,有
-
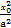=1.
由题意又有
·
=,
可得a2=5b2,c2=a2+b2=6b2,则e=
=.
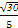(2)联立方程得
得4x2-10cx+35b2=0,
设A(x1,y1),B(x2,y2),
则
设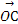=(x3,y3),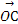=λ+,
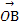即
又C为双曲线E上一点,即
-5
=5b2,
有(λx1+x2)2-5(λy1+y2)2=5b2,
化简得:λ2(
-5
)+(
-5
)+2λ(x1x2-5y1y2)=5b2,
又A(x1,y1),B(x2,y2)在双曲线E上,
所以-5=5b2,-5=5b2.
又x1x2-5y1y2=x1x2-5(x1-c)(x2-c)
=-4x1x2+5c(x1+x2)-5c2=10b2,
得:λ2+4λ=0,解出λ=0或λ=-4.
列方程求解.(2)联立方程,设出A,B,
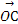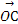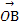的坐标,代入=λ+求解.解：(1)由点P(x0,y0)(x0≠±a)在双曲线
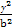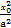-=1上,有-=1.由题意又有
·=,可得a2=5b2,c2=a2+b2=6b2,则e=
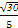=.(2)联立方程得
得4x2-10cx+35b2=0,
设A(x1,y1),B(x2,y2),
则
设
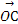=(x3,y3),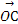=λ+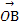,即
又C为双曲线E上一点,即
-5=5b2,有(λx1+x2)2-5(λy1+y2)2=5b2,
化简得:λ2(
-5)+(-5)+2λ(x1x2-5y1y2)=5b2,又A(x1,y1),B(x2,y2)在双曲线E上,
所以
-5=5b2,-5=5b2.又x1x2-5y1y2=x1x2-5(x1-c)(x2-c)
=-4x1x2+5c(x1+x2)-5c2=10b2,
得:λ2+4λ=0,解出λ=0或λ=-4.
练习册系列答案
名校课堂系列答案
相关题目
,则C的实轴长为( )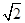
(B)2
-
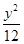=1的左焦点,A(1,4),P是双曲线右支上的动点,则|PF|+|PA|的最小值为 .
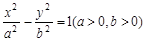的两条渐近线将平面划分为“上、下、左、右”四个区域（不含边界），若点(1,2)在“上”区域内，则双曲线离心率的取值范围为 。
-
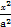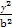=1(a>0,b>0)的一条渐近线方程为y=
x,则双曲线的离心率为( )
－
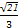
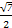
＝1的左支上，则
＝________．
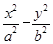＝1(a>0，b>0)的两个焦点，过左焦点F1的直线l与双曲线C的左、右两支分别交于A，B两点．若|AB|∶|BF2|∶|AF2|＝3∶4∶5，则双曲线的离心率是( )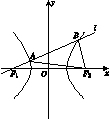
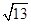
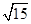
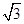
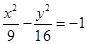，有以下说法：①实轴长为6；②双曲线的离心率是
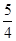；③焦点坐标为（±5，0）；④渐近线方程是
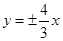，⑤焦点到渐近线的距离等于3。正确的说法是 ，（把所有正确的说法序号都填上）