题目内容
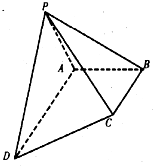 (2012•桂林模拟)在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD=2,底面ABCD是直角梯形,BC∥AD,AB⊥AD,AD=2AB=2BC=2
(2012•桂林模拟)在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD=2,底面ABCD是直角梯形,BC∥AD,AB⊥AD,AD=2AB=2BC=2| 2 |
(1)求证:AB⊥平面PAD;
(2)求二面角A-PD-C的余弦值.
分析:(1)利用面面垂直的性质,证明线面垂直;
(2)先作出面面角,并给予证明,再计算其余弦值即可.
(2)先作出面面角,并给予证明,再计算其余弦值即可.
解答:(1)证明:∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,AB⊥AD
∴AB⊥平面PAD;
(2)设AD的中点为O,PD的中点为M,连接OC,OM,CM
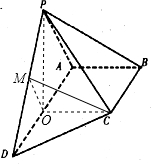
∵PA=PD=2,∴PO⊥AD
在直角梯形ABCD中,BC∥AD,AB⊥AD,AD=2AB=2BC=2
∴OC⊥AD,AO=OD=
∴PO=OD=
∴OM⊥PD
∵Rt△POD≌Rt△POC
∴PO=PC-CD=2
∴CM⊥PD
∴∠OMC为二面角A-PD-C的平面角
∵AB⊥AD,OC∥AB
∴OC⊥OM
∵OM=1,CM=
∴cos∠OMC=
=
∴二面角A-PD-C的余弦值为
.
∴AB⊥平面PAD;
(2)设AD的中点为O,PD的中点为M,连接OC,OM,CM

∵PA=PD=2,∴PO⊥AD
在直角梯形ABCD中,BC∥AD,AB⊥AD,AD=2AB=2BC=2
| 2 |
∴OC⊥AD,AO=OD=
| 2 |
∴PO=OD=
| 2 |
∴OM⊥PD
∵Rt△POD≌Rt△POC
∴PO=PC-CD=2
∴CM⊥PD
∴∠OMC为二面角A-PD-C的平面角
∵AB⊥AD,OC∥AB
∴OC⊥OM
∵OM=1,CM=
| 3 |
∴cos∠OMC=
| OM |
| CM |
| ||
| 3 |
∴二面角A-PD-C的余弦值为
| ||
| 3 |
点评:本题考查线面垂直,考查面面角,解题的关键是掌握面面垂直的性质,正确作出面面角,属于中档题.

练习册系列答案
相关题目
 (2012•桂林模拟)如图,已知球O是棱长为1 的正方体ABCD-A1B1C1D1的内切球,则平面ACD1截球o的截面面积为
(2012•桂林模拟)如图,已知球O是棱长为1 的正方体ABCD-A1B1C1D1的内切球,则平面ACD1截球o的截面面积为