题目内容
例2:(1)设不等式2( )2+9
)2+9 +9≤0时,求
+9≤0时,求 的最大值和最小值.
的最大值和最小值.(2)设f(x)=|lgx|,a、b是满足
 的实数,其中0<a<b
的实数,其中0<a<b①求证:a<1<b;②求证:2<4b-b2<3.
【答案】分析:(1)、由不等式2( )2+9
)2+9 +9≤0,可知
+9≤0,可知 ,从而导出
,从而导出 .再由
.再由 =(log2x-1)•(log2x-3)=(log2x)2-4log2x+3=(log2x-2)2-1可以导出f(x)最大值和最小值.
=(log2x-1)•(log2x-3)=(log2x)2-4log2x+3=(log2x-2)2-1可以导出f(x)最大值和最小值.
(2):①由f(x)=|lgx|,f(a)=f(b)可知|lga|=|lgb|.再由0<a<b,y=lgx是增函数,可知-lga=lgb,由此可证a<1<b.
②由 可知
可知 ,由此可证2<4b-b2<3.
,由此可证2<4b-b2<3.
解答:解:(1)、∵不等式2( )2+9
)2+9 +9≤0,∴
+9≤0,∴ ,∴
,∴ .∴
.∴ .
.
∴ =(log2x-1)•(log2x-3)=(log2x)2-4log2x+3=(log2x-2)2-1.
=(log2x-1)•(log2x-3)=(log2x)2-4log2x+3=(log2x-2)2-1.
故当log2x=2时, 的最小值是-1;当log2x=0时,
的最小值是-1;当log2x=0时, 的最大值是3.
的最大值是3.
(2)、①证明:∵f(x)=|lgx|,f(a)=f(b),∴|lga|=|lgb|.
∵0<a<b,y=lgx是增函数,∴-lga=lgb,故a<1<b.
②证明:∵-lga=lgb,∴ ,∴ab=1,
,∴ab=1,
∵0<a<b,∴ .
.
∵ ,∴
,∴ ,∴
,∴ .
.
∴ ,∴
,∴ ,∵b>1,∴2<4b-b2<3.
,∵b>1,∴2<4b-b2<3.
点评:注意对数的性质运用及对数方程的解法.
 )2+9
)2+9 +9≤0,可知
+9≤0,可知 ,从而导出
,从而导出 .再由
.再由 =(log2x-1)•(log2x-3)=(log2x)2-4log2x+3=(log2x-2)2-1可以导出f(x)最大值和最小值.
=(log2x-1)•(log2x-3)=(log2x)2-4log2x+3=(log2x-2)2-1可以导出f(x)最大值和最小值.(2):①由f(x)=|lgx|,f(a)=f(b)可知|lga|=|lgb|.再由0<a<b,y=lgx是增函数,可知-lga=lgb,由此可证a<1<b.
②由
 可知
可知 ,由此可证2<4b-b2<3.
,由此可证2<4b-b2<3.解答:解:(1)、∵不等式2(
 )2+9
)2+9 +9≤0,∴
+9≤0,∴ ,∴
,∴ .∴
.∴ .
.∴
 =(log2x-1)•(log2x-3)=(log2x)2-4log2x+3=(log2x-2)2-1.
=(log2x-1)•(log2x-3)=(log2x)2-4log2x+3=(log2x-2)2-1.故当log2x=2时,
 的最小值是-1;当log2x=0时,
的最小值是-1;当log2x=0时, 的最大值是3.
的最大值是3.(2)、①证明:∵f(x)=|lgx|,f(a)=f(b),∴|lga|=|lgb|.
∵0<a<b,y=lgx是增函数,∴-lga=lgb,故a<1<b.
②证明:∵-lga=lgb,∴
 ,∴ab=1,
,∴ab=1,∵0<a<b,∴
 .
.∵
 ,∴
,∴ ,∴
,∴ .
.∴
 ,∴
,∴ ,∵b>1,∴2<4b-b2<3.
,∵b>1,∴2<4b-b2<3.点评:注意对数的性质运用及对数方程的解法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 )2+9
)2+9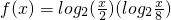 的最大值和最小值.
的最大值和最小值.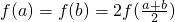 的实数,其中0<a<b
的实数,其中0<a<b