Question

在△ABC中，∠A，∠B的对边分别为a，b，且∠A=60°，b=4，若满足条件的△ABC有且只有1个，则a的取值范围是

 

．

Answer 1

分析：先通过正弦定理得出a与sinB的关系式，再通过∠A=60°求出B的取值范围，设t=sinB画出图象．要满足条件的△ABC有且只有1个，只需方程t=sinB有且只有一个根．通过观察图象求出t的范围进而求出a的范围．

解答：解：根据正弦定理

a

sinA

=

b

sinB

∴a=

b

sinB

•sinA=

4

sinB

•

3

2

=

2 3

sinB

∵∠A+∠B+∠C=180°
∴∠B=180°-∠A-∠C=180°-60°-∠C=120°-∠C
∴0＜∠B＜120°
设t=sinB，
要满足条件的△ABC有且只有1个，则有y=t和y=sinB的图象只有一个交点．其图象如下图．

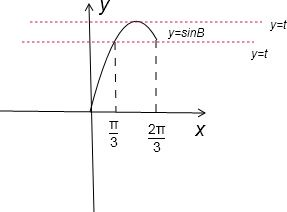
只有当B=

π

2

或0＜B＜

π

3

时，
即sinB=1或0＜sinB≤

3

2

时，方程t=sinB，只有一个根．
∴对于方程a=

2 3

sinB

，

2 3

sinB

=2

3

或

2 3

sinB

≥4时，有且只有一个根．
∴满足条件的△ABC有且只有1个，则a的取值范围是a=2

3

或a≥4
故选A=2

3

或a≥4

点评：本题主要考查了正弦定理的应用．当问题不好解决的时候，可试着用数形结合的方法．