题目内容
(本小题满分12分)在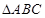 中,
中, 分别为内角
分别为内角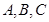 的对边,且
的对边,且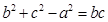 。
。
(Ⅰ)求角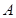 的大小;
的大小;
(Ⅱ)设函数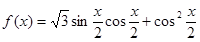 ,求
,求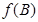 的最大值,并判断此时
的最大值,并判断此时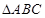 的形状.
的形状.
(Ⅰ) (Ⅱ)
(Ⅱ)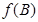 最大值是
最大值是 ,△ABC为等边三角形.
,△ABC为等边三角形.
解析试题分析:(Ⅰ)在△ABC中,因为b2+c2-a2=bc,由余弦定理 a2= b2+c2-2bccosA 可得cosA= .
.
∵ 0<A<π , (或写成A是三角形内角) ∴ .
.
(Ⅱ)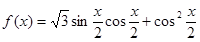

 ,
,
∵ ∴
∴
∴
∴当 ,即
,即 时,
时,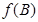 有最大值是
有最大值是 .
.
又∵ ,
,
∴ ∴△ABC为等边三角形.
∴△ABC为等边三角形.
考点:余弦定理及三角函数性质(最大值)
点评:解三角形时应用正余弦定理实现边角的互相转化,三角函数性质的考查要结合图像分析求解

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,且
,且 ,其中
,其中 是
是 的内角,
的内角, 是角
是角 的大小;
的大小; ,求
,求 的内角A、B、C的对边分别为
的内角A、B、C的对边分别为 ,
,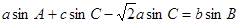
 ,
,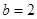 ,求
,求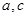
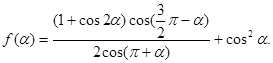
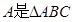 的内角,且为钝角,求
的内角,且为钝角,求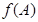 的最小值;
的最小值; 是锐角
是锐角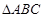 的内角,且
的内角,且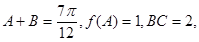 求
求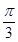 )+sin2x.
)+sin2x.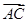 ·
·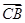 =
=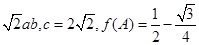 , 求△ABC的面积S.
, 求△ABC的面积S.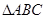 中,角
中,角 的对边分别是
的对边分别是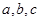 已知向量
已知向量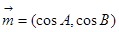
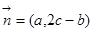 ,且
,且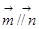 .
.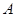 的大小;
的大小; 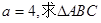 面积的最大值。
面积的最大值。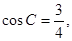
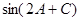 的值。
的值。 中,角
中,角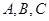 所对的边为
所对的边为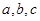 ,已知
,已知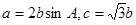
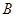 的值;
的值; ,求
,求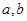 的值
的值 中,
中,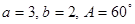 ,求
,求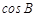 及
及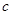 的值.
的值.