Question

（本小题共13分）

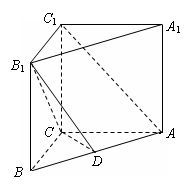
直三棱柱ABC-A₁B₁C₁中，AB=5，AC=4，BC=3，AA₁=4，D是AB的中点．

（Ⅰ）求证：AC⊥B₁C；

（Ⅱ）求证：AC₁∥平面B₁CD；

Answer 1

（本小题满分13分）

直三棱柱ABC-A₁B₁C₁中，AB=5，AC=4，BC=3，AA₁=4，D点在线段AB上．

（Ⅰ）求证：AC⊥B₁C；  （Ⅱ）若D是AB中点，求证：AC₁∥平面B₁CD；

证明：（Ⅰ）在△ABC中，因为  AB=5，AC=4，BC=3，

           所以  AC⊥BC．         

因为  直三棱柱ABC-A₁B₁C₁，所以  C C₁⊥AC．        

因为  BC∩AC =C，   所以 AC⊥平面B B₁C₁C．  

所以  AC⊥B₁C．         ………………………7分

（Ⅱ）连结BC₁，交B₁C于E．

因为  直三棱柱ABC-A₁B₁C₁，

所以  侧面B B₁C₁C为矩形，且E为B₁C中点．              

又D是AB中点，所以 DE为△ABC₁的中位线，  所以 DE// AC₁．

因为  DE平面B₁CD， AC₁平面B₁CD，                  

所以  AC₁∥平面B₁CD．                                    ………………………13分