Question

函数f（x）是R上的奇函数，其部分图象如图，试用图象写出不等式x•f（x）≤0的解集为    ．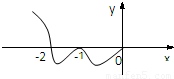

Answer 1

【答案】分析：根据奇函数的图象关于原点对称，可画出函数的图象，然后数形结合，分x≥0和x＜0时，两种情况讨论不等式的解集，最后综合讨论结果可得答案．
解答：解：∵函数f（x）是R上的奇函数，
∴函数f（x）的图象如下图所示：

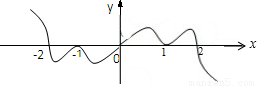
由图可知：
当x≥0时，若x•f（x）≤0，则x≥2，或x=1，或x=0
当x＜0时，若x•f（x）≤0，则x≤-2，或x=-1，
综上不等式x•f（x）≤0的解集为{x|x≤-2，或x≥2或x=±1或x=0}
故答案为：{x|x≤-2，或x≥2或x=±1或x=0}
点评：本题考查的知识点是函数的奇偶性与函数的单调性，其中根据已知函数的部分图象和奇函数的图象关于原点对称画出函数的图象是解答的关键．