题目内容
如图,用半径为R的圆铁皮,剪一个圆心角为α的扇形,制成一个圆锥形的漏斗,问圆心角α取什么值时,漏斗容积最大.(圆锥体积公式: ,其中圆锥的底面半径为r,高为h)
,其中圆锥的底面半径为r,高为h)
【答案】分析:设圆锥的底面半径为r,高为h,体积为V,求出r2+h2=R2,表示出体积表达式,利用导数求出函数的最大值,得到结果.
解答:解:设圆锥的底面半径为r,高为h,体积为V,那么r2+h2=R2,
因此,
= =
= .…(3分)
.…(3分) .
.
令V'=0,即 ,得
,得 .…(5分)
.…(5分)
当 时,V'>0.
时,V'>0.
当 时,V'<0.
时,V'<0.
所以, 时,V取得极大值,并且这个极大值是最大值.…(8分)
时,V取得极大值,并且这个极大值是最大值.…(8分)
把 代入r2+h2=R2,得
代入r2+h2=R2,得 .
.
由Ra=2πr,得
答:圆心角α为 弧度时,漏斗容积最大.…(12分)
弧度时,漏斗容积最大.…(12分)
点评:本题考查圆锥与扇形展开图的关系,体积的计算,考查计算能力,导数的应用,必须注意函数的单调性与最值的关系.
解答:解:设圆锥的底面半径为r,高为h,体积为V,那么r2+h2=R2,
因此,

=
 =
= .…(3分)
.…(3分) .
.令V'=0,即
 ,得
,得 .…(5分)
.…(5分)当
 时,V'>0.
时,V'>0.当
 时,V'<0.
时,V'<0.所以,
 时,V取得极大值,并且这个极大值是最大值.…(8分)
时,V取得极大值,并且这个极大值是最大值.…(8分)把
 代入r2+h2=R2,得
代入r2+h2=R2,得 .
.由Ra=2πr,得

答:圆心角α为
 弧度时,漏斗容积最大.…(12分)
弧度时,漏斗容积最大.…(12分)点评:本题考查圆锥与扇形展开图的关系,体积的计算,考查计算能力,导数的应用,必须注意函数的单调性与最值的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
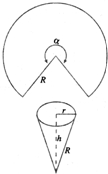 如图,用半径为R的圆铁皮,剪一个圆心角为α的扇形,制成一个圆锥形的漏斗,问圆心角α取什么值时,漏斗容积最大.(圆锥体积公式:
如图,用半径为R的圆铁皮,剪一个圆心角为α的扇形,制成一个圆锥形的漏斗,问圆心角α取什么值时,漏斗容积最大.(圆锥体积公式: 的扇形,制成一个圆锥形的漏斗,问圆心角
的扇形,制成一个圆锥形的漏斗,问圆心角 ,其中圆锥的底面半径为r,高为h)
,其中圆锥的底面半径为r,高为h)
 如图,用半径为R的圆铁皮,剪一个圆心角为α的扇形,制成一个圆锥形的漏斗,问圆心角α取什么值时,漏斗容积最大.(圆锥体积公式:
如图,用半径为R的圆铁皮,剪一个圆心角为α的扇形,制成一个圆锥形的漏斗,问圆心角α取什么值时,漏斗容积最大.(圆锥体积公式: ,其中圆锥的底面半径为r,高为h)
,其中圆锥的底面半径为r,高为h) 如图,用半径为R的圆铁皮,剪一个圆心角为
如图,用半径为R的圆铁皮,剪一个圆心角为