题目内容
在下列4个函数:①y=sin| x |
| 2 |
| π |
| 2 |
分析:根据正弦函数的最小正周期T=
求得①②中函数的最小正周期,可判断其正误;结合正弦函数的单调性可判断③;根据余弦函数的最小正周期和单调性可判断④.
| 2π |
| w |
解答:解:y=sin
的最小正周期T=
=4π,不符合要求;
y=sinx的最小正周期T=2π,不符合题意;
y=-tanx的最小正周期T=π但是在(0,
)上单调递减,不符合题意;
y=-cos2x的最小正周期T=
=π,令2kπ≤2x≤π+2kπ,∴kπ≤x≤
+kπ
∴y=-cos2x在[kπ,
+kπ]上单调递增,故在区间(0,
)上增,满足条件.
故答案为:④
| x |
| 2 |
| 2π | ||
|
y=sinx的最小正周期T=2π,不符合题意;
y=-tanx的最小正周期T=π但是在(0,
| π |
| 2 |
y=-cos2x的最小正周期T=
| 2π |
| 2 |
| π |
| 2 |
∴y=-cos2x在[kπ,
| π |
| 2 |
| π |
| 2 |
故答案为:④
点评:本题主要考查正弦函数、正切函数和余弦函数的最小正周期的求法和单调性.考查三角函数的基本性质的应用.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
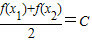 成立(其中C为常数),则称函数y=f(x)在D上的均值为C,现在给出下列4个函数:①y=x3②y=4sinx③y=lgx④y=2x,则在其定义域上的均值为 2的所有函数是下面的( )
成立(其中C为常数),则称函数y=f(x)在D上的均值为C,现在给出下列4个函数:①y=x3②y=4sinx③y=lgx④y=2x,则在其定义域上的均值为 2的所有函数是下面的( )