题目内容
若函数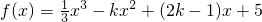 在区间(2,3)上是减函数,则k的取值范围是________.
在区间(2,3)上是减函数,则k的取值范围是________.
k≥2
分析:先由函数求导,再由“函数f(x)在区间(2,3)内是减函数”转化为“f'(x)=x2-2kx+2k-1≤0在(2,3)恒成立”,进一步转化为最值问题:2k≥x+1在(2,3)恒成立,求得函数x+1的最大值即可.
解答: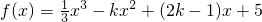 求导:f'(x)=x2-2kx+2k-1,
求导:f'(x)=x2-2kx+2k-1,
f'(x)=x2-2kx+2k-1≤0在(2,3)恒成立.
即2k(x-1)≥(x-1)(x+1)在(2,3)恒成立.
即2k≥x+1在(2,3)恒成立.
所以2k≥4,?k≥2,k的取值范围是[2,+∞).
故答案为:k≥2.
点评:本题考查利用导数研究函数的单调性,求解本题的关键是正确求出函数的导数,关键是把函数是减函数的性质转化为函数恒成立的问题,转化思想在高中数学在应用很广泛.
分析:先由函数求导,再由“函数f(x)在区间(2,3)内是减函数”转化为“f'(x)=x2-2kx+2k-1≤0在(2,3)恒成立”,进一步转化为最值问题:2k≥x+1在(2,3)恒成立,求得函数x+1的最大值即可.
解答:
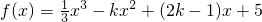 求导:f'(x)=x2-2kx+2k-1,
求导:f'(x)=x2-2kx+2k-1,f'(x)=x2-2kx+2k-1≤0在(2,3)恒成立.
即2k(x-1)≥(x-1)(x+1)在(2,3)恒成立.
即2k≥x+1在(2,3)恒成立.
所以2k≥4,?k≥2,k的取值范围是[2,+∞).
故答案为:k≥2.
点评:本题考查利用导数研究函数的单调性,求解本题的关键是正确求出函数的导数,关键是把函数是减函数的性质转化为函数恒成立的问题,转化思想在高中数学在应用很广泛.

练习册系列答案
相关题目
若函数![]() 在区间(2,3)上是减函数,则k的取值范围是( )
在区间(2,3)上是减函数,则k的取值范围是( )
|
| A. | [1,+∞) | B. | [0,1] | C. | (﹣∞,0] | D. | [2,+∞) |
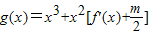 在区间(2,3)上不单调,求m的范围.
在区间(2,3)上不单调,求m的范围.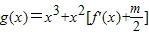 在区间(2,3)上不单调,求m的范围.
在区间(2,3)上不单调,求m的范围. 在区间(2,3)上是减函数,则k的取值范围是( )
在区间(2,3)上是减函数,则k的取值范围是( ) 在区间(2,3)上是减函数,则k的取值范围是 .
在区间(2,3)上是减函数,则k的取值范围是 .