题目内容
若函数 在区间(2,3)上是减函数,则k的取值范围是( )
在区间(2,3)上是减函数,则k的取值范围是( )A.[1,+∞)
B.[0,1]
C.(-∞,0]
D.[2,+∞)
【答案】分析:由题意可得f′(x)≤0在(2,3)上恒成立.令g(x)=x2-2kx+(2k-1),则 ,解出即可.
,解出即可.
解答:解:f′(x)=x2-2kx+(2k-1),
∵函数 在区间(2,3)上是减函数,∴f′(x)≤0在(2,3)上恒成立.
在区间(2,3)上是减函数,∴f′(x)≤0在(2,3)上恒成立.
即x2-2kx+(2k-1)≤0在(2,3)上恒成立.
令g(x)=x2-2kx+(2k-1),则 ,解得k≥2.
,解得k≥2.
故选D.
点评:熟练掌握利用导数研究函数的单调性、二次函数的性质是解题的关键.
 ,解出即可.
,解出即可.解答:解:f′(x)=x2-2kx+(2k-1),
∵函数
 在区间(2,3)上是减函数,∴f′(x)≤0在(2,3)上恒成立.
在区间(2,3)上是减函数,∴f′(x)≤0在(2,3)上恒成立.即x2-2kx+(2k-1)≤0在(2,3)上恒成立.
令g(x)=x2-2kx+(2k-1),则
 ,解得k≥2.
,解得k≥2.故选D.
点评:熟练掌握利用导数研究函数的单调性、二次函数的性质是解题的关键.

练习册系列答案
相关题目
若函数![]() 在区间(2,3)上是减函数,则k的取值范围是( )
在区间(2,3)上是减函数,则k的取值范围是( )
|
| A. | [1,+∞) | B. | [0,1] | C. | (﹣∞,0] | D. | [2,+∞) |
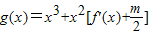 在区间(2,3)上不单调,求m的范围.
在区间(2,3)上不单调,求m的范围.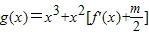 在区间(2,3)上不单调,求m的范围.
在区间(2,3)上不单调,求m的范围. 在区间(2,3)上是减函数,则k的取值范围是 .
在区间(2,3)上是减函数,则k的取值范围是 .