题目内容

函数f（x）对一切实数x、y均有f（x+y）-f（y）=（x+2y+1）x成立,且f（1）=0.

（1）求f（0）的值；

（2）当f（x）+2＜logax,x∈（0,）恒成立时,求a的取值范围.

思路分析：本题是量词与不等式的综合题，它含有的量词是“对一切”是全称量词，因此在解决时，可以利用特殊值法.

解：（1）由已知等式f（x+y）-f（y）=（x+2y+1）·x,

    令x=1,y=0,得f（1）-f（0）=2.又因为f（1）=0,所以f（0）=-2.

（2）由（1）,知f（0）=-2.所以f（x）+2=f（x）-f（0）=f（x+0）-f（0）=（x+1）·x.

    因为x∈（0,）,所以f（x）+2∈（0,）.

    要使x∈（0,）时,f（x）+2＜logax恒成立,显然当a＞1时不可能.

    所以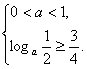解得.

方法归纳 在解决此类问题时，可以利用特殊值法，对于恒成立的问题，可以转化为求函数的最值的问题.

练习册系列答案
相关题目
函数f（x）对一切实数x，y均有f（x+y）-f（y）=（x+2y+1）x成立，且f（1）=0，
（1）求f（0）的值．
（2）对任意的x1∈(0，
1
2
)，x2∈(0，
1
2
)，都有f（x1）+2＜logax2成立时，求a的取值范围．
已知函数f（x）对一切实数x，y均有f（x+y）-f（y）=x（x+2y+1）成立，且f（1）=0．
（1）求f（0）的值        
（2）求f（x）的解析式
（3）若函数g（x）=（x+1）f（x）-a[f（x+1）-x]在区间（-1，2）上是减函数，求实数a的取值范围．
定义在R上的函数f（x），如果存在函数g（x）=kx+b（k，b为常数），使得f（x）≥g（x）对一切实数x都成立，则称g（x）为f（x）的一个承托函数．现有如下命题：
①对给定的函数f（x），其承托函数可能不存在，也可能无数个；
②g（x）=2x为函数f（x）=2x的一个承托函数；
③若函数g（x）=x-a为函数f（x）=ax2的承托函数，则a的取值范围是a≥
12
；
④定义域和值域都是R的函数f（x）不存在承托函数；
其中正确命题的序号是
①③
①③
．
已知函数f（x）对一切实数x，y都有f（x+y）-f（y）=x（x+2y+5）成立，且f（1）=0．
（1）求f（0）的值，并求f（x）的解析式；
（2）若函数g（x）=f（x）-ax在区间[-2，2]上是单调函数，求实数a的取值范围；
（3）已知：当0＜x＜
12
时，不等式f（x）+3＜2x+m恒成立，求实数m的取值范围．
已知函数f（x）对一切实数x，y均有f（x+y）-f（y）=x（x+2y+1）成立，且f（1）=0，
（1）求f（0）的值；
（2）求f（x）的解析式；
（3）函数g（x）=xf（x+x）在[0，2]上何处取得极值，最值是多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网