题目内容
已知函数![]()
(Ⅰ)求函数的单调区间;
(Ⅱ)a为何值时,方程![]() 有三个不同的实根.
有三个不同的实根.
解:(Ⅰ)![]()
由![]() 得
得![]() 由
由![]() 得
得![]()
∴![]() 在
在![]() 单调递增;
单调递增;![]() 在
在![]() 单调递减
单调递减
(Ⅱ)由(Ⅰ)知![]() ,
,![]()
![]() 有三个不同的实根,则
有三个不同的实根,则![]() 解得
解得![]()
∴当![]() 时
时![]() 有三个不同的实根
有三个不同的实根
【解析】(1)由![]() 得,
得, ![]() ,而
,而![]() ,所以
,所以![]() .由
.由![]() 得,
得, ![]() ,所以
,所以![]() .又由
.又由![]() 得,
得,![]() ,所以
,所以![]() .
.
(2)猜想![]() .
.
①当![]() 时,
时,![]() ,猜想成立;
,猜想成立;
②假设![]() 时猜想成立,即
时猜想成立,即![]() ,则当
,则当![]() 时,
时,![]()
![]() .
.
即![]()
![]()
化简得![]() ,解得
,解得![]() ,
,
即![]() 时猜想成立,由①、②知
时猜想成立,由①、②知![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

 的定义域;
的定义域; 为何值时,函数值大于1.
为何值时,函数值大于1.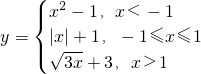 编写一程序求函数值.
编写一程序求函数值. 编写一程序求函数值.
编写一程序求函数值. 编写一程序求函数值.
编写一程序求函数值.