题目内容
14、（选做题）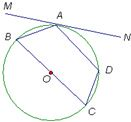
如图，四边形ABCD内接于⊙O，BC是直径，MN与⊙O相切，切点为A，∠MAB=35°，则∠D=
如图，四边形ABCD内接于⊙O，BC是直径，MN与⊙O相切，切点为A，∠MAB=35°，则∠D=125°
．分析：由已知中，MN与⊙O相切，切点为A，我们易根据弦切角定理，得到∠D=∠NAB，由已知中∠MAB=35°，由邻补角定理，我们易求出∠NAB的大小，进而求出∠D．
解答：解：连接OA，由于A是切点，故OA⊥MN
∵∠MAB=35°，
∴∠BAO=55°，
又MN与⊙O相切，切点为A，
又由弦切角定理，我们可得
∠AOB=70°
故∠B=55°
∴则∠D=125°
故答案为：125°
∵∠MAB=35°，
∴∠BAO=55°，
又MN与⊙O相切，切点为A，
又由弦切角定理，我们可得
∠AOB=70°
故∠B=55°
∴则∠D=125°
故答案为：125°
点评：本题考查的知识点是弦切角定理，邻补角的性质，其中由弦切角定理，得到∠AOB=70°，是解答本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
15、选做题：如图，点A、B、C是圆O上的点，且AB=4，∠ACB=30°，则圆O的面积等于
（2012•深圳一模）（几何证明选讲选做题）如图4，A，B是圆O上的两点，且OA⊥OB，OA=2，C为OA的中点，连接BC并延长交圆O于点D，则CD=
（几何证明选讲选做题）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，直线MN切⊙O于D，∠MDA=60°，则∠BCD=
请考生在下列两题中任选一题作答，若两题都做，则按所做的第一题评阅计分．
（2010•陕西一模）（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分．）