题目内容
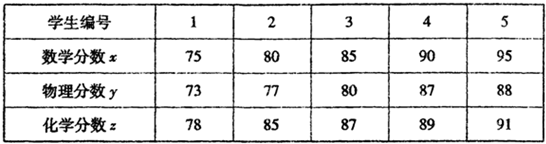
为了对某校高三(1)班9月调考成绩进行分析,在全班同学中随机抽出5位,他们的数学分数、物理分数、化学分数(均已折算为百分制)对应如下表:
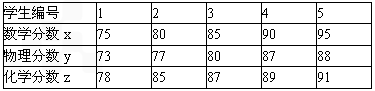
(I)求这5位同学中数学和物理分数都不小于85分的概率;
(II)从散点图分析,y与x、x与x之间都有较好的线性相关关系,分别求y与x、z与x的线性回归方程,并用相关指数比较所求回归模型的拟合效果.
(II)从散点图分析,y与x、x与x之间都有较好的线性相关关系,分别求y与x、z与x的线性回归方程,并用相关指数比较所求回归模型的拟合效果.
解:(I)这5位同学中数学和物理分数都不小于85分,共有2人,故概率为P= ;
;
(II)设y与x、z与x的线性回归方程分别是′ =bx+a、
=bx+a、 =b′x+a′,
=b′x+a′,
根据所给的数据,可以计算出b= =0.8,a=81﹣0.8×85=13,
=0.8,a=81﹣0.8×85=13,
b′= =0.6,a′=86﹣0.6×85=35.
=0.6,a′=86﹣0.6×85=35.
∴ =0.8x+13、
=0.8x+13、 =0.6x+35,
=0.6x+35,
∴ (yi﹣
(yi﹣ )2=02+02+(﹣1)2+22+(﹣1)2=6,
)2=02+02+(﹣1)2+22+(﹣1)2=6,
∴ (zi﹣
(zi﹣ )2=(﹣2)2+22+12+02+(﹣1)2=10,
)2=(﹣2)2+22+12+02+(﹣1)2=10,
又y与x、z与x的相关指数是R2=1﹣ ≈0.964、R′2=1﹣
≈0.964、R′2=1﹣ ≈0.90.
≈0.90.
故回归模型 =0.8x+13比回归模型
=0.8x+13比回归模型 =0.6x+35的拟合的效果好.
=0.6x+35的拟合的效果好.
 ;
;(II)设y与x、z与x的线性回归方程分别是′
 =bx+a、
=bx+a、 =b′x+a′,
=b′x+a′,根据所给的数据,可以计算出b=
 =0.8,a=81﹣0.8×85=13,
=0.8,a=81﹣0.8×85=13,b′=
 =0.6,a′=86﹣0.6×85=35.
=0.6,a′=86﹣0.6×85=35.∴
 =0.8x+13、
=0.8x+13、 =0.6x+35,
=0.6x+35,∴
 (yi﹣
(yi﹣ )2=02+02+(﹣1)2+22+(﹣1)2=6,
)2=02+02+(﹣1)2+22+(﹣1)2=6,∴
 (zi﹣
(zi﹣ )2=(﹣2)2+22+12+02+(﹣1)2=10,
)2=(﹣2)2+22+12+02+(﹣1)2=10,又y与x、z与x的相关指数是R2=1﹣
 ≈0.964、R′2=1﹣
≈0.964、R′2=1﹣ ≈0.90.
≈0.90.故回归模型
 =0.8x+13比回归模型
=0.8x+13比回归模型 =0.6x+35的拟合的效果好.
=0.6x+35的拟合的效果好.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 ,
, 2=250,
2=250, ,
, ,
,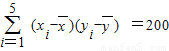 ,
, .
.